TABELLA RIASSUNTIVA DELLE FORMULE DI GONIOMETRICHE
Dopo aver visto tutte le FORMULE GONIOMETRICHE in questa tabella andiamo a riepilogarle tutte rimandando la loro dimostrazione alle rispettive lezioni.
FORMULE DI ADDIZIONE E SOTTRAZIONE | |
|---|---|
| FORMULA DI | FORMULA |
| Addizione del seno | sen (α + β) = sen α · cos β + cos α · sen β |
| Sottrazione del seno | sen (α - β) = sen α · cos β - cos α · sen β |
| Addizione del coseno | cos(α + β) = cos α · cos β - sen α · sen β |
| Sottrazione del coseno | cos (α - β) = cos α · cos β + sen α · sen β |
| Addizione della tangente | 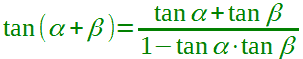 α + β ≠ (π/2) + kπ α ≠ (π/2) + kπ β ≠ (π/2) + kπ con k ∈ Z |
| Sottrazione della tangente | 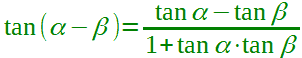 α + β ≠ (π/2) + kπ α ≠ (π/2) + kπ α ≠ (π/2) + kπ con k ∈ Z |
| Addizione della cotangente | 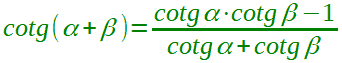 α + β ≠ kπ α ≠ kπ α ≠ kπ con k ∈ Z |
| Sottrazione della cotangente | 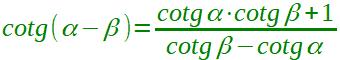 α + β ≠ kπ α ≠ kπ α ≠ (kπ con k ∈ Z |
FORMULE DI DUPLICAZIONE | |
|---|---|
| FORMULA DI DUPLICAZIONE | FORMULA |
| duplicazione del seno | sen 2α = 2 sen α · cos α |
| duplicazione del coseno | cos 2α = cos2 α - sen2 α cos 2α = 1 - 2 sen2 α cos 2α = 2 cos2 α - 1 |
| duplicazione della tangente | 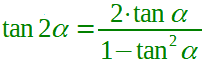 α ≠ ± (π/4) + kπ α ≠ (π/2) + kπ con k ∈ Z |
| duplicazione della cotangente | 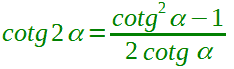 α ≠ (π/2) + kπ α ≠ kπ con k ∈ Z |
FORMULE DI TRIPLICAZIONE | |
|---|---|
| FORMULA DI TRIPLICAZIONE | FORMULA |
| triplicazione del seno | sen 3α = 3 sen α - 4 sen3 α |
| triplicazione del coseno | cos 3α = 4 cos3 α - 3 cos α |
| triplicazione della tangente | 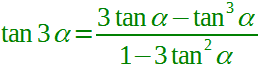 α ≠ (π/2) + kπ con k ∈ Z |
| triplicazione della cotangente | 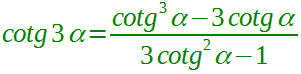 α ≠ kπ con k ∈ Z |
FORMULE DI BISEZIONE | |
|---|---|
| FORMULA DI BISEZIONE | FORMULA |
| bisezione del seno | 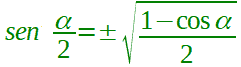 |
| bisezione del coseno | 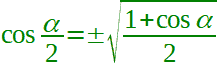 |
| bisezione della tangente | 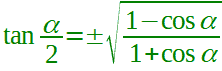 α ≠ 2kπ con k ∈ Z 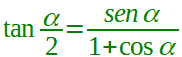 α ≠ π + 2kπ con k ∈ Z 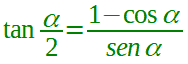 α ≠ 2kπ con k ∈ Z |
| bisezione della cotangente | 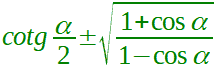 α ≠ 2kπ con k ∈ Z 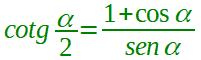 α ≠ kπ con k ∈ Z 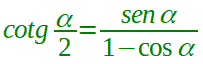 α ≠ 2kπ con k ∈ Z |
FORMULE PARAMETRICHE | |
|---|---|
| FORMULA PARAMETRICA | FORMULA |
| Formula parametrica del seno | 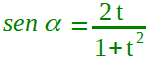 con t = tan α/ 2 α ≠ π + 2kπ con k ∈ Z |
| Formula parametrica del coseno | 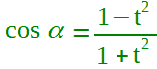 con t = tan α/ 2 α ≠ π + 2kπ con k ∈ Z |
FORMULE DI PROSTAFERESI | |
|---|---|
| FORMULA DI PROSTAFERESI | FORMULA |
| prostaferesi per il seno | 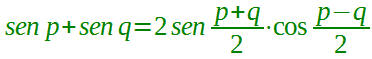 |
| prostaferesi per il seno | 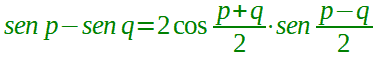 |
| prostaferesi per il coseno | 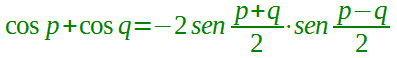 |
| prostaferesi per il coseno | 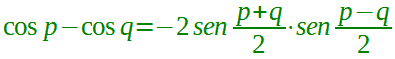 |
| prostaferesi per la tangente | 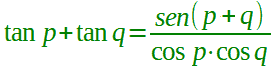 p ≠ (π/2) + kπ q ≠ (π/2) + kπ con k ∈ Z |
| prostaferesi per la tangente | 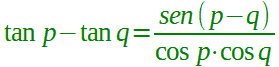 p ≠ (π/2) + kπ q ≠ (π/2) + kπ con k ∈ Z |
| prostaferesi per la cotangente | 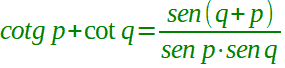 p ≠ kπ q ≠ kπ con k ∈ Z |
| prostaferesi per la cotangente | 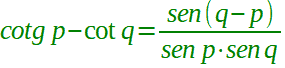 p ≠ kπ q ≠ kπ con k ∈ Z |
FORMULE DI WERNER | |
|---|---|
| FORMULA DI WERNER | FORMULA |
| Formula di Werner | 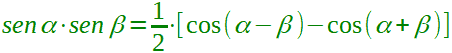 |
| Formula di Werner | 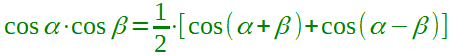 |
| Formula di Werner | 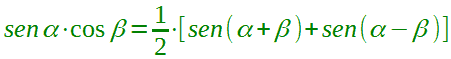 |
| Formula di Werner | 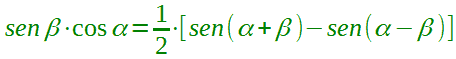 |






