L'INSIEME DEI NUMERI INTERI RELATIVI
Nella lezione precedente abbiamo osservato che la sottrazione NON E' UN'OPERAZIONE INTERNA in N.
Infatti, affinché la sottrazione tra due numeri naturali, a e b, sia eseguibile nell'insieme N è necessario che a sia uguale o maggiore di b. Ovvero:
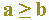
che si legge
a è maggiore o uguale a b.
Da questa considerazione nasce la necessità di ampliare l'insieme N in un nuovo insieme, che è l'insieme Z.
L'insieme Z è l'insieme dei NUMERI INTERI RELATIVI. Esso viene denominato anche, più semplicemente, insieme dei NUMERI INTERI.
Quindi l'insieme Z è dato da:
Z = {..., -5, -4, -3, -2, -1, 0, +1, +2, +3, +4, +5, ...}.
I numeri naturali preceduti dal segno più formano l'insieme dei NUMERI INTERI POSITIVI che indichiamo con
Z+
che si legge
zeta più
e rappresenta
l'insieme dei numeri interi positivi.
Quindi:
Z+ = {+1, +2, +3, +4, +5......}
che si legge
l'insieme Z più formato dagli elementi +1, +2, +3, +4, +5,...
I numeri naturali preceduti dal segno meno formano l'insieme dei NUMERI INTERI NEGATIVI che indiciamo con
Z-
che si legge
zeta meno
e rappresenta
l'insieme dei numeri interi negativi.
Quindi:
Z- = {-1, -2, -3, -4, -5......}
che si legge
l'insieme Z meno formato dagli elementi -1, -2, -3, -4, -5,...
I due insiemi Z+ e Z- formano complessivamente l'insieme dei numeri interi Z.
Ora esaminiamo meglio l'insieme dei numeri interi positivi:
Z+ = { +1, +2, +3, +4 ......}
Ora stabiliamo che, quando non vi siano possibilità di equivoco, i numeri interi positivi possono essere scritti senza il segno che li precede. In altre parole:
+1 = 1
+2 = 2
+3 = 3
.....
Quindi possiamo scrivere l'insieme dei numeri interi positivi nel modo seguente:
Z+ = { 1, 2, 3, 4 ......}.
E' evidente, allora che
Z+ = N
Infatti
N = { 1, 2, 3, 4 ......}.
In altre parole possiamo dire che l'INSIEME DEI NUMERI INTERI POSITIVI coincide con l'INSIEME DEI NUMERI NATURALI.
Di conseguenza possiamo anche dire che l'insieme N è un sottoinsieme dell'insieme Z:
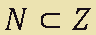
Per questa ragione si usa dire che N è IMMERSO in Z.






