FORMULE DI WERNER
- Formula di addizione del seno
- Formula di sottrazione del seno
- Formula di addizione del coseno
- Formula di sottrazione del coseno
- Formule di prostaferesi per il seno
- Formule di prostaferesi per il coseno
Si chiamano FORMULE DI WERNER una serie di formule che permettono di TRASFORMARE il PRODOTTO di due funzioni goniometriche nella SOMMA o nella DIFFERENZA di funzioni goniometriche. Quindi possiamo dire che esse risolvono il problema inverso rispetto alle formule di prostaferesi.
Andiamo a vedere quali sono e a dimostrarle qui di seguito, precisando che tutte le dimostrazioni di queste formule si basano sull'uso delle
FORMULE DI ADDIZIONE E SOTTRAZIONE.
Iniziamo dalla prima formula. Vogliamo trovare una formula che ci permetta di risolvere il seguente prodotto:
sen α · sen β
Andiamo a scrivere la FORMULA di SOTTRAZIONE del COSENO:
cos (α - β) = cos α · cos β + sen α · sen β
Ora scriviamo la FORMULA di ADDIZIONE del COSENO:
cos (α + β) = cos α · cos β - sen α · sen β
SOTTRAIAMO membro a membro ed otteniamo:
cos (α - β) - cos (α + β) = cos α · cos β + sen α · sen β - ( cos α · cos β - sen α · sen β)
da cui otteniamo:
cos (α - β) - cos (α + β) = cos α · cos β + sen α · sen β - cos α · cos β + sen α · sen β
Eseguendo le somme algebriche si ha:
cos (α - β) - cos (α + β) = 2 sen α · sen β
Scambiamo i due membri:
2 sen α · sen β = cos (α - β) - cos (α + β)
e dividiamo per 2 in modo da ottenere la formula cercata:
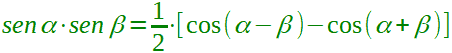
Passiamo alla seconda formula di Werner. Vogliamo trovare una formula che ci permetta di risolvere il seguente prodotto:
cos α · cos β
Esattamente come abbiamo fatto prima, anche questa volta, andiamo a scrivere la FORMULA di SOTTRAZIONE del COSENO:
cos (α - β) = cos α · cos β + sen α · sen β
e poi la FORMULA di ADDIZIONE del COSENO:
cos (α + β) = cos α · cos β - sen α · sen β
Questa volta, però, SOMMIAMO membro a membro ed otteniamo:
cos (α - β) + cos (α + β) = cos α · cos β + sen α · sen β + cos α · cos β - sen α · sen β
Eseguendo le somme algebriche si ha:
cos (α - β) + cos (α + β) = 2 cos α · cos β
Scambiamo i due membri:
2 cos α · cos β = cos (α - β) + cos (α + β)
e dividiamo per 2 in modo da ottenere la formula cercata:
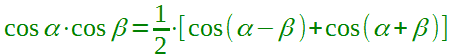
Chiaramente la formula può essere scritta anche nel modo seguente:
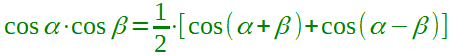
che è poi il modo in cui la trovate scritta in tutti i libri di testo.
Veniamo alla terza formula di Werner. Vogliamo trovare una formula che ci permetta di risolvere il seguente prodotto:
sen α · cos β
Questa volta, nella dimostrazione, usiamo le FORMULE di ADDIZIONE e SOTTRAZIONE del SENO.
Iniziamo con lo scrivere la FORMULA di ADDIZIONE del SENO:
sen (α + β) = sen α · cos β + cos α · sen β
Poi scriviamo la FORMULA di SOTTRAZIONE del SENO:
sen (α - β) = sen α · cos β - cos α · sen β
Andiamo a SOMMARE membro a membro ed otteniamo:
sen (α + β) + sen (α - β) = senα · cos β + cos α · sen β + sen α · cos β - cos α · sen β
Eseguendo le somme algebriche si ha:
sen(α + β) + sen (α - β) = 2 sen α · cos β
Scambiamo i due membri:
2 sen α · cos β = sen (α + β) + sen (α - β)
e dividiamo per 2 in modo da ottenere la formula cercata:
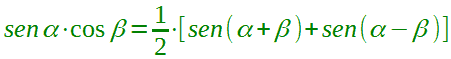
In genere, nella maggior parte dei libri di testo, si cosiderano queste tre formule di Werner: in realtà si potrebbe usare anche una quarta formula, ovvero quella che ci permette di trovare:
cos α · sen β
Allora voi direte: "Perché, allora, generalmente viene omessa?" La rispsota è: "Perché usare questa formula oppure quella che abbiamo appena visto sopra (cioè quella del prodotto del seno di α per il coseno di β) è del tutto indifferente e porta allo stesso risultato: si tratta di due modi diversi di esprimere il prodotto del seno di un angolo per il coseno di un altro".
Per completezza di esposizione, andiamo comunque a spiegare qual è la formula da applicare e come si giunge ad essa.
Anche in questo caso partiamo dalla FORMULA di ADDIZIONE del SENO:
sen (α + β) = sen α · cos β + cos α · sen β
Poi scriviamo la FORMULA di SOTTRAZIONE del SENO:
sen (α - β) = sen α · cos β - cos α · sen β
Quindi andiamo a SOTTRARRE membro a membro ed otteniamo:
sen (α + β) - sen (α - β) = senα · cos β + cos α · sen β - ( sen α · cos β - cos α · sen β)
Da cui otteniamo:
sen (α + β) - sen (α - β) = senα · cos β + cos α · sen β - sen α · cos β + cos α · sen β
Eseguendo le somme algebriche si ha:
sen(α + β) - sen (α - β) = 2 cos α · cos β
Scambiamo i due membri:
2 cos α · cos β = sen (α + β) - sen (α - β)
e dividiamo per 2 in modo da ottenere la formula cercata:
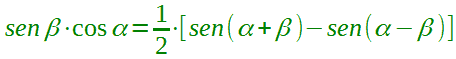
Un'ultima precisazione su questo argomento: spesso si legge che la dimostrazione di queste formule si basa sull'uso delle formule di prostaferesi. Ad essere più precisi la dimostrazione di queste formule si basa su alcune RELAZIONI usate nella DIMOSTRAZIONE delle formule di prostaferesi. Infatti:
- la relazione
2 sen α · sen β = cos (α - β) - cos (α + β)
da cui abbiamo ottenuto la prima delle formule di Werner qui esaminte, era stata ottenuta anche nella dimostrazione delle formule di prostaferesi per il coseno;
- la relazione
2 cos α · cos β = cos (α - β) + cos (α + β)
da cui abbiamo ottenuto la seconda delle formule di Werner qui esaminte, era stata ottenuta anche nella dimostrazione delle formule di prostaferesi per il coseno;
- la relazione
2 sen α · cos β = sen (α + β) + sen (α - β)
da cui abbiamo ottenuto la terza delle formule di Werner qui esaminte, era stata ottenuta anche nella dimostrazione delle formule di prostaferesi per il seno;
- la relazione
2 cos α · cos β = sen (α + β) - sen (α - β)
da cui abbiamo ottenuto l'ultima delle formule di Werner esaminte in questa lezione, era stata ottenuta anche nella dimostrazione delle formule di prostaferesi per il seno.






