FORMULA DI DUPLICAZIONE DELLA COTANGENTE
Continuiamo a parlare delle formule di duplicazione ed occupiamoci, in questa lezione, della FORMULA DI DUPLICAZIONE DELLA COTANGENTE: in altre parole andremo a vedere come possiamo esprimere la cotangente dell'angolo 2α in funzione dell'angolo α.
Quindi, cominciamo scrivendo:
cotg 2α
L'angolo 2α può essere scritto come (α + α) e di conseguenza:
cotg 2α = cotg (α + α)
La formula di addizione della cotangente ci dice che:
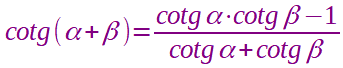
Sostituendo questa formula nella prima, avremo:
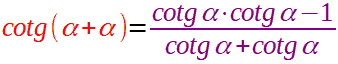
Eseguiamo il prodotto indicato a numeratore e sommiamo i termini simili a denominatore:
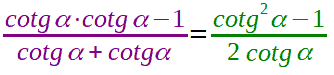
Trattandosi di una frazione occorre porre come condizioni di esistenza della stessa, che il denominatore sia diverso da zero per evitare che la frazione perda di significato. Quindi dobbiamo porre come condizione:
2 cotg α ≠ 0
il che equivale a dire che
cotg α ≠ 0
Dallo studio delle funzioni goniometriche sappiamo che la cotangente di un angolo è pari a 0 quando l'angolo è pari a π/2, a (3/2)π, ecc...: quindi in altre parole quando l'angolo è pari a (π/2) + kπ.
Pertanto, la condizione di esistenza da porre è:
α ≠(π/2) + kπ.
con k ∈ Z
Dobbiamo però ricordare anche che la COTANGENTE non è altro che il RAPPORTO tra il COSENO e il SENO dell'angolo. Di conseguenza dobbiamo porre come ulteriore condizione che il denominatore di tale frazione, ovvero il SENO dell'angolo α sia diverso da zero:
sen α ≠ 0
il che accade ogni 180° a partire dall'angolo di ampiezza 0. Pertanto possiamo scrivere la seconda condizione di esistenza nel modo seguente:
α ≠ kπ
con k ∈ Z
Ricapitolando la FORMULA DI DUPLICAZIONE DELLA COTANGENTE è:
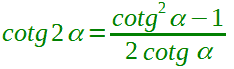
le cui condizioni di esistenza sono:
α ≠ (π/2) + kπ
α ≠ kπ
con k ∈ Z
Così come accade per la tangente, anche per la cotangente esiste anche un altro modo per dimostrare come si giunge alla sua formula di duplicazione: ne parleremo nella prossima lezione.






