FORMULE DI PROSTAFERESI PER IL COSENO
- Formula di addizione del coseno
- Formula di sottrazione del coseno
- Formule di prostaferesi per il seno
Continuiamo a parlare delle formule di prostaferesi occupandoci, in questa lezione, delle FORMULE DI PROSTAFERESI per il COSENO.
Cominciamo con lo scrivere la FORMULA DI ADDIZIONE del COSENO:
cos (α + β) = cos α · cos β - sen α · sen β
Ora scriviamo la FORMULA DI SOTTRAZIONE del COSENO:
cos (α - β) = cos α · cos β + sen α · sen β
Mettiamo a sistema le due equazioni e SOMMIAMO membro a membro:
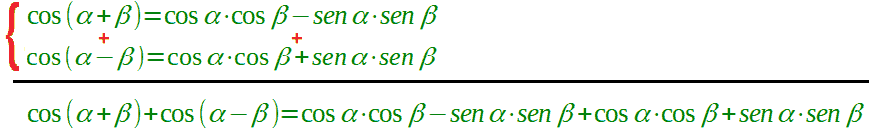
Ora andiamo a semplificare ed otteniamo:
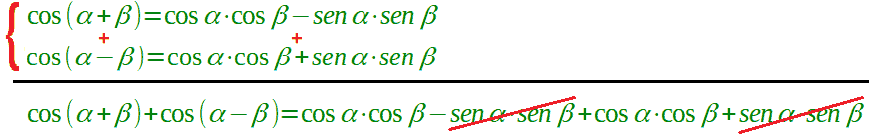
Sommiamo i termini simili ed abbiamo:
cos (α + β) + cos (α - β) = - 2 sen α · sen β
Ora, esattamente come abbiamo fatto per il seno, poniamo:
α + β = p
e
α - β = q
E andiamo a cercare il valore di α e quello di β.
Mettiamo a sistema le due relazioni scritte:
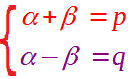
e ricaviamo il valore di α e di β. I passaggi sono stati già illustrati nella lezione precedente, alla quale rimandiamo:
I valori che si ottengono sono:
α = (p + q)/ 2
β = (p - q)/ 2
Ora torniamo alla formula:
cos (α + β) + cos (α - β) = -2 sen α · sen β
Poiché abbiamo detto che:
α + β = p
α - β = q
α = (p + q)/ 2
β = (p - q)/ 2
andiamo a sostituire nella formula precedente ed otteniamo:
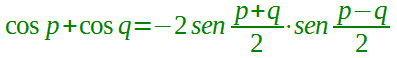
Abbiamo così ottenuto una delle due formule di prostaferesi per il coseno che spesso viene detta anche TERZA FORMULA DI PROSTAFERESI
Ora andiamo a cercare la seconda formula di prostaferersi per il coseno, quella relativa al alla differenza tra il coseno di due angoli.
Partiamo sempre dalla FORMULA DI ADDIZIONE del COSENO:
cos (α + β) = cos α · cos β - sen α · sen β
e dalla FORMULA DI SOTTRAZIONE del COSENO:
cos (α - β) = cos α · cos β + sen α · sen β
Mettiamo a sistema le due equazioni e, questa volta, SOTTRAIAMO membro a membro:
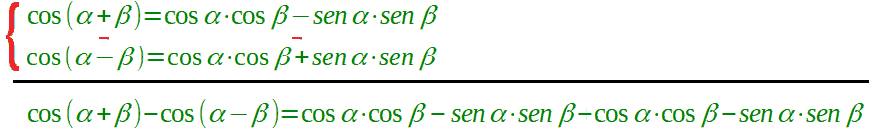
Ora andiamo a semplificare:
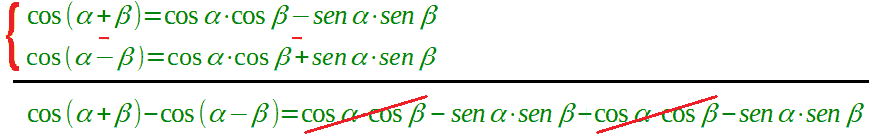
e sommiamo i termini simili:
cos (α + β) - cos (α - β) = -2 sen α · sen β
Ora poniamo:
α + β = p
e
α - β = q
E andiamo a cercare il valore di α e quello di β come abbiamo già visto in precedenza:
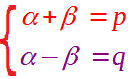
Di conseguenza avremo che:
α + β = p
α - β = q
α = (p + q)/ 2
β = (p - q)/ 2
andiamo a sostituire nella formula precedente ed otteniamo:
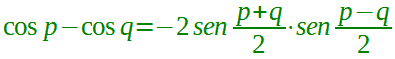
Quella che abbiamo appena scritto è la seconda formula di prostaferesi per il coseno. Spesso viene detta anche QUARTA FORMULA DI PROSTAFERESI.
Nella prossima lezione vedremo le formule di prostaferersi per la tangente.






