EQUAZIONI IRRAZIONALI CONTENENTI RADICALI CON INDICI DIVERSI
- Equazioni irrazionali
- Dominio di un'equazione irrazionale
- Come si risolvono le equazioni irrazionali
- Equazioni irrazionali risolvibili in modo immediato
- Equazioni irrazionali contenenti radicali quadratici
- Equazioni irrazionali contenenti radicali quadratici
- Equazioni irrazionali contenenti radicali quadratici
- Risoluzione di equazioni irrazionali con un solo radicale di indice pari
- Risoluzione di equazioni irrazionali con un solo radicale di indice pari
- Risoluzione di equazioni irrazionali con un solo radicale di indice pari
- Risoluzione di equazioni irrazionali con due radicali di indice pari
- Risoluzione di equazioni irrazionali con tre o più radicali di indice pari
- Risoluzione di equazioni irrazionali con radicali multipli
- Equazioni irrazionali contenenti radicali cubici
- Equazioni irrazionali fratte
- Elevamento a potenza
- Equazioni equivalenti
Fino a qui abbiamo esaminato EQUAZIONI IRRAZIONALI contenenti radicali sempre dello stesso indice: cioè l'equazione irrazionale conteneva sempre solo radicali quadratici o solo radicali cubici.
Vediamo ora cosa accade quando l'equazione irrazionale contiene due o più radicali aventi indici diversi.
Ad esempio l'equazione si presenta nel modo seguente:
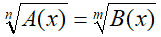
Per risolvere questo tipo di equazione occorre ELEVARE entrambi i membri ad una POTENZA pari al minimo comune multiplo degli INDICI dei radicali. Supponiamo che, tale m.c.m. sia
n·m
Una volta fatto l'elevamento a potenza si tratterà di risolvere nei modi consueti.
Ottenuto il risultato, o i risultati, occorrerà verificare che essi siano anche delle SOLUZIONI ACCETTABILI dell'equazione di partenza.
In alternativa si possono porre le condizioni affinché la soluzione ottenuta sia accettabile: in questo caso, per comprendere quali equazioni occorre impostare nel sistema, dobbiamo distinguere l'ipotesi che gli indici dei radicali siano pari oppure dispari.
Se, sia n che m sono DISPARI, la soluzione dell'equazione si ottiene semplicemente elevando entrambi i termini alla
n·m
ovvero
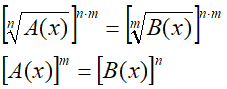
Le soluzioni trovate saranno, tutte, anche soluzioni dell'equazione di partenza.
Se, sia n che m sono PARI, si deve porre come condizione che entrambi i radicandi siano positivi o uguali a zero. Pertanto occorrerà impostare il seguente sistema
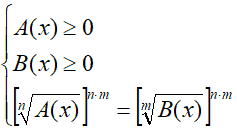
Esempio:
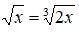
Nel nostro caso gli indici sono, uno pari e uno dispari. Per non complicarci troppo la vita e per non correre il rischio di impostare delle condizioni sbagliate decidiamo di optare per il metodo della verifica.
Innanzitutto cerchiamo le soluzioni.
Partiamo col trovare il m.c.m. tra 2 e 3: esso è 6.
Quindi eleviamo entrambi i membri dell'equazione a 6:
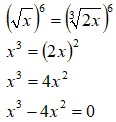
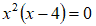
Per la legge di annullamento del prodotto, il nostro prodotto è nullo quando:
x2 = 0
oppure quando
x - 4 = 0.
Risolviamo le due equazioni.
Partiamo dalla prima
x2 = 0
x = 0.
Passiamo alla seconda
x - 4 = 0
x = 4.
Ora verifichiamo le due soluzioni ottenute.
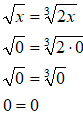
La soluzione
x = 0
è accettabile.
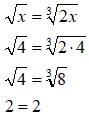
Anche la soluzione
x = 4
è accettabile.






