EQUAZIONI IRRAZIONALI FRATTE
- Equazioni irrazionali
- Dominio di un'equazione irrazionale
- Come si risolvono le equazioni irrazionali
- Equazioni irrazionali risolvibili in modo immediato
- Equazioni irrazionali contenenti radicali quadratici
- Equazioni irrazionali contenenti radicali quadratici
- Equazioni irrazionali contenenti radicali quadratici
- Risoluzione di equazioni irrazionali con un solo radicale di indice pari
- Risoluzione di equazioni irrazionali con un solo radicale di indice pari
- Risoluzione di equazioni irrazionali con un solo radicale di indice pari
- Risoluzione di equazioni irrazionali con due radicali di indice pari
- Risoluzione di equazioni irrazionali con tre o più radicali di indice pari
- Risoluzione di equazioni irrazionali con radicali multipli
- Equazioni irrazionali contenenti radicali cubici
- Campo di esistenza di una frazione algebrica
Un'EQUAZIONE IRRAZIONALE si dice FRATTA quando a DENOMINATORE troviamo un RADICALE il cui radicando contiene l'incognita.
Esempi:
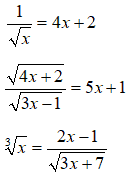
Queste sono tutte equazioni irrazionali fratte.
Ora chiediamoci: "Come si risolvono le equazioni irrazionali fratte?".
Come sempre possiamo optare per due metodi:
- il primo metodo consiste nel cercare le soluzioni dell'equazione e nell'effettuare, successivamente, la VERIFICA andando a sostituire tali soluzioni nell'equazione di partenza in modo da vedere quali sono le soluzioni accettabili e quali quelle estranee;
- il secondo metodo consiste nel porre, prima di risolvere l'equazione, le CONDIZIONI affinché i risultati trovati non siano estranei all'equazione di partenza. Usando questo secondo metodo, sarà importante distinguere il caso in cui i radicali indicati nell'equazione abbiano indice pari da quello in cui essi abbiano indice dispari poiché cambiano, come abbiamo visto nelle lezioni precedenti, le condizioni da porre. Alle solite condizioni, che valgono per tutte le equazioni irrazionali, occorre AGGIUNGERE quella che il DENOMINATORE sia DIVERSO DA ZERO.
Vediamo, come occorre procedere attraverso un esempio.
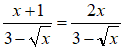
Utilizziamo il secondo metodo, e cominciamo col vedere quali sono le condizioni da porre affinché le soluzioni trovate siano accettabili.
Poiché i radicali presenti hanno indice pari, dobbiamo porre come condizioni che i radicandi siano pari o maggiori di zero. I due radicandi sono uguali quindi dovremo porre una sola condizione, ovvero:
x ≥ 0
Poiché nell'equazione sono presenti due frazioni, dobbiamo aggiungere anche la condizione che i denominatori delle frazioni siano diversi da zero. Essendo i denominatori delle due frazioni uguali, porremo una sola condizione, cioè:
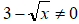
Andiamo a vedere quando, questa condizione si verifica:
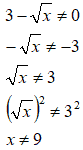
Quindi, il denominatore della frazione si annulla per
x = 9
Di conseguenza noi dovremo andare a prendere i valori diversi da 9.
Il sistema che dobbiamo risolvere, quindi, è
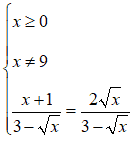
Risolviamo l'ultima equazione:
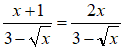
Moltiplichiamo entrambi i membri dell'equazione per
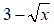
ed otteniamo
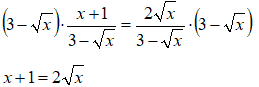
Ora eleviamo al quadrato entrambi i membri dell'equazione, in modo da eliminare la radice a secondo membro, e risolviamo nei modi consueti:
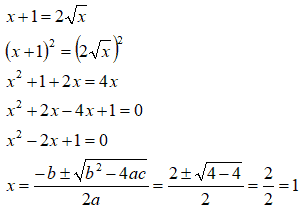
Scriviamo anche questa soluzione nel nostro sistema e avremo:
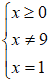
Il risultato trovato
x = 1
è maggiore di zero ed è, al tempo stesso, diverso da 9: quindi la nostra soluzione è accettabile.






