RISOLUZIONE DI EQUAZIONI IRRAZIONALI CON TRE O PIU' RADICALI DI INDICE PARI
- Equazioni irrazionali
- Dominio di un'equazione irrazionale
- Come si risolvono le equazioni irrazionali
- Equazioni irrazionali risolvibili in modo immediato
- Equazioni irrazionali contenenti radicali quadratici
- Equazioni irrazionali contenenti radicali quadratici
- Equazioni irrazionali contenenti radicali quadratici
- Risoluzione di equazioni irrazionali con un solo radicale di indice pari
- Risoluzione di equazioni irrazionali con un solo radicale di indice pari
- Risoluzione di equazioni irrazionali con un solo radicale di indice pari
- Risoluzione di equazioni irrazionali con due radicali di indice pari
- Prodotto tra radicali
Continuiamo l'esame dei diversi tipi di EQUAZIONI IRRAZIONALI con RADICALI QUADRATICI.
Qualora ci dovessimo trovare di fronte ad equazioni del tipo:
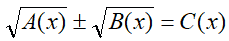
oppure
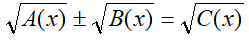
o ancora
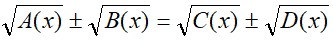
occorrerebbe imporre molte condizioni. Per questa ragione può essere più comodo cercare le soluzioni dell'equazione e successivamente andare a verificarle.
Esempio:
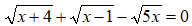
Per prima cosa vediamo quali sono le condizioni di esistenza dei vari radicali:
x + 4 ≥ 0
ovvero
x ≥ -4
x - 1 ≥ 0
x ≥ 1
x ≥ 0
Quindi, affinché tutti e tre i radicali abbiamo significato è necessario che
x ≥ 1
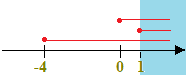
Torniamo alla nostra equazione: ci conviene trasportare uno dei radicali a secondo membro in modo da isolarlo. In questa maniera, elevando ambo i membri al quadrato, almeno un radicale verrà eliminato.
Quindi avremo:
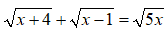
Ora eleviamo primo e secondo membro al quadrato:
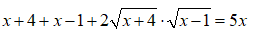
Sommiamo i termini simili ed eseguiamo il prodotto dei radicali, indicato a primo membro:
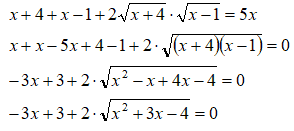
Ora isoliamo il radicale portandolo a secondo membro e successivamente eleviamo, primo e secondo membro, al quadrato:
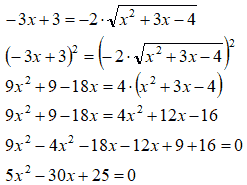
Andiamo a cercare il valore di x:
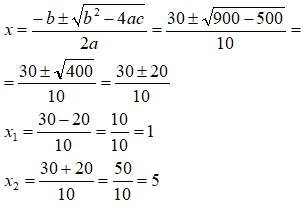
Entrambe le soluzioni trovate rispettano la condizione di essere maggiori o uguali ad 1.
Andiamo a verificare se esse sono soluzioni dell'equazione data.
Partiamo da
x = 1
sostituiamo nell'equazione data è abbiamo:
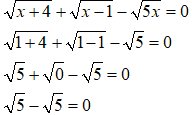
Quindi la soluzione è accettabile.
Passiamo a verificare la seconda soluzione
x = 5.
Abbiamo
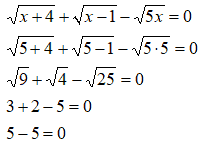
Anche questa soluzione è accettabile.
Quindi, entrambe le soluzioni trovate, sono soluzioni della nostra equazione irrazionale di partenza.






