PROPRIETA' SIMMETRICA DI UNA RELAZIONE IN UN INSIEME
- Nozione di insieme
- Coppie ordinate
- Relazione di un insieme A in un insieme B
- Relazione tra insiemi
- Rappresentazione grafica di una relazione
- Relazione tra insiemi: ulteriori considerazioni
- Grafico di una relazione
- Relazioni inverse
- Rappresentazione grafica di una relazione inversa
- Composizione di relazioni
- Relazioni in un insieme
- Rappresentazione di una relazioni in un insieme
- Relazione inversa in un insieme
- Implicazione logica
- Proprietà delle relazioni su un insieme
- Proprietà riflessiva di una relazione in un insieme
- Proprietà antisimmetrica
- Proprietà transitiva
Consideriamo l'insieme A:
A = {a, b, c, d}.
Sia 
la relazione rappresentata dalle coppie dell'insieme 
:
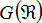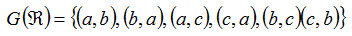
Ora rappresentiamo la relazione con il DIAGRAMMA
A FRECCE
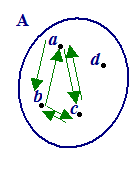
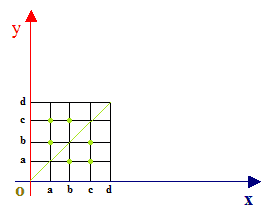
e con il DIAGRAMMA CARTESIANO.
Nel DIAGRAMMA A FRECCE si nota che, ogni volta che vi è una freccia che va da un elemento di A verso un altro, vi è anche una freccia che va da quest'ultimo al primo.
Quindi possiamo affermare che la
relazione
è SIMMETRICA.
Nel DIAGRAMMA CARTESIANO notiamo che tutti i punti della relazione sono simmetrici rispetto alla DIAGONALE, che abbiamo evidenziato con una linea verde.
Quindi possiamo affermare che la relazione
è SIMMETRICA.
Pertanto possiamo
dire che, una RELAZIONE
in un insieme A
è SIMMETRICA
se:
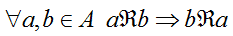
che si legge
se per qualunque a e b appartenenti ad A, a associato b mediante R allora b associato a mediante R.
Di conseguenza, una RELAZIONE in UN INSIEME NON è SIMMETRICA se vi è anche solo una coppia degli elementi dell'insieme tali che il primo è in relazione con il secondo, ma il secondo non è in relazione con il primo.
