COMPOSIZIONE DI RELAZIONI
- Nozione di insieme
- Relazione di un insieme A in un insieme B
- Relazione tra insiemi
- Rappresentazione grafica di una relazione
- Relazione tra insiemi: ulteriori considerazioni
- Grafico di una relazione
- Relazioni inverse
- Rappresentazione grafica di una relazione inversa
- Implicazione logica
Consideriamo i seguenti insiemi:
A = {12, 5}
B = {6, 0}
C
= {2, 1}.
Possiamo dire che
12 è il doppio di 6
e che
6 è il triplo di 2.
Potremmo anche dire che:
12 è il doppio del triplo di 2.
Generalizzando, se abbiamo:
- un generico elemento a che appartiene all'insieme A;
- un generico elemento b che appartiene all'insieme B;
- un generico elemento c che appartiene all'insieme C;
- e a
è associato a b
mediante la relazione
 ;
; - e
b è associato
a c
mediante la relazione
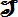 ;
;
esiste una RELAZIONE
COMPOSTA di A in C.
Quindi
possiamo dire che, dati tre insiemi A,
B, C,
se RELAZIONE di A
in B e
RELAZIONE di B
in C vi
è una RELAZIONE
di A
in C che si dice RELAZIONE
COMPOSTA delle relazioni  e
e 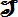 e si indica con
e si indica con
che si legge
S composto R.
Pertanto posto che
ne segue che
che si legge
se a associato b mediante R
e b associato c mediante S allora
a associato c mediante S composto con R.
Facciamo ora due osservazioni:
- Attenzione all'ordine con il quale
sono indicate le due relazioni
- Notiamo che:
- la relazione
 è un sottoinsieme di AxB;
è un sottoinsieme di AxB; - la relazione
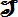 è un sottoinsieme di BxC;
è un sottoinsieme di BxC; - la relazione
è un sottoinsieme di AxC.
- la relazione






