RELAZIONE TRA INSIEMI: ULTERIORI CONSIDERAZIONI
Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:
- Nozione di insieme
- Relazione di un insieme A in un insieme B
- Relazione tra insiemi
- Rappresentazione grafica di una relazione
Continuiamo a parlare della RELAZIONE TRA INSIEMI.
Consideriamo gli insiemi:
A = {1, 4, 6}
B = {2, 5}.
Vogliamo vedere se ci sono degli elementi di A legati agli elementi di B dalla relazione "è multiplo di", e se si quali sono.
Per RAPPRESENTARE GRAFICAMENTE la RELAZIONE tra A e B utilizziamo una TABELLA A DOPPIA ENTRATA.
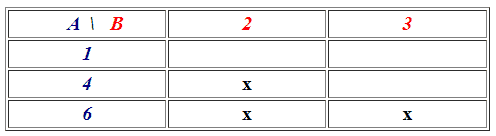
Notiamo che:
- vi è un elemento di A,( il 4) che è associato ad un solo elemento di B ( il 2);
- vi è un elemento di A,( il 6) che è associato a due elementi di B ( il 2 e il 3);
- vi è un elemento di A, ( l'1) che non è associato a nessun elemento di B.
Ora consideriamo gli insiemi:
A = {2, 5}
B = {9, 10}.
Vogliamo vedere se ci sono degli elementi di A legati agli elementi di B dalla relazione "è divisore di", e se si quali sono.
Costruiamo la TABELLA A DOPPIA ENTRATA.
Notiamo che:
- vi sono due elementi di A, ( il 2 e il 5) che sono associati ad uno stesso elemento di B ( il 10)
- vi è un elemento di B, ( il 9) a cui non è associato a nessun elemento di A.
Gli esempi fatti ci portano ad affermare che:
- un elemento di A può essere associato ad un solo elemento di B, a più elementi di B o a nessun elemento di B;
- più elementi di A possono essere associati ad uno stesso elemento di B;
- vi può essere un qualche elemento di B che non è associato a nessun elemento di A.
