IMPLICAZIONE LOGICA
Continuiamo l'esame delle OPERAZIONI con le PROPOSIZIONI: e parliamo della IMPLICAZIONE LOGICA.
Supponiamo di avere le seguenti due proposizioni, che chiameremo rispettivamente p e q:
p = Giovanni è abruzzese
q = Giovanni è italiano.
Possiamo affermare che
se Giovanni è abruzzese, allora Giovanni è italiano.
Questa frase, nel linguaggio matematico, viene scritta cosi:

che si legge
se Giovanni è abruzzese allora Giovanni è italiano
oppure
Giovanni è abruzzese implica che Giovanni è italiano.
Il
segno:

è
detto segno di implicazione e si legge implica.
Se
scriviamo
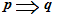
la proposizione
p (cioè quella scritta prima del segno di implicazione) è detta ANTECEDENTE
mentre la proposizione
q (cioè quella scritta dopo il segno di implicazione) è detta CONSEGUENTE.

A volte, al posto del simbolo appena visto, troviamo anche il simbolo
→
anche
questo è un simbolo di implicazione, ma viene più propriamente usato per
indicare l'implicazione materiale e non quella logica di cui noi
stiamo parlando in questo contesto.
Torniamo al nostro esempio
p = Giovanni è abruzzese;
q = Giovanni è italiano
p implica q = se Giovanni è abruzzese allora Giovanni è italiano.
Se Giovanni è abruzzese sicuramente Giovanni è anche italiano e, quindi, se è vera la proposizione p, ed è vera la proposizione q, è vera anche la proposizione p implica q.
Esaminiamo ora un altro esempio:
p = Giovanni è abruzzese;
q = Giovanni non è italiano
p implica q = se Giovanni è abruzzese allora Giovanni non è italiano.
Se Giovanni è abruzzese sicuramente Giovanni è anche italiano e, quindi, se è vera la proposizione p, ed è falsa la proposizione q, è falsa anche la proposizione p implica q.
Ricapitolando
- p
VERA
q VERA
p implica q VERA
-
p
VERA
q FALSA
p implica q FALSA
Quindi possiamo dire che date due proposizioni p e q, diremo che p implica q è vera se, dall'essere vera p segue che è vera anche q.






