ARCHI CHE DIFFERISCONO DI 3π/2
In questa lezione esamineremo gli archi associati che differiscono di 3π/2, in altre parole vedremo la relazione esistente tra le funzioni goniometriche dell'angolo α e dell'angolo (3π/2) + α.
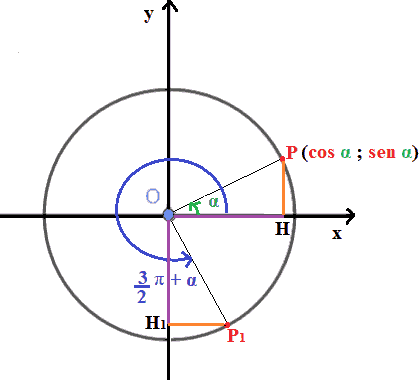
Il modo di procedere è sempre lo stesso: disegnamo la circonferenza goniometrica, l'angolo orientato α e chiamiamo P il punto associato a tale angolo.
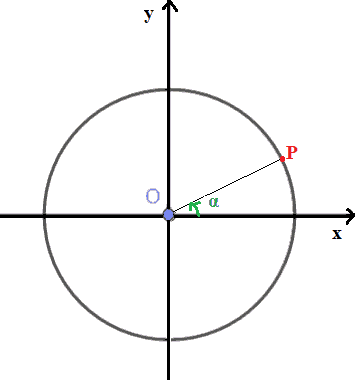
Sempre sulla stessa circonferenza goniometrica, individuiamo l'angolo orientato 3π/2, in altre parole l'angolo di 270°
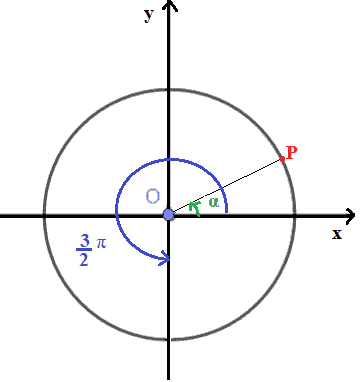
e, ad esso, aggiungiamo l'angolo α in modo da ottenere l'angolo (3π/2) + α
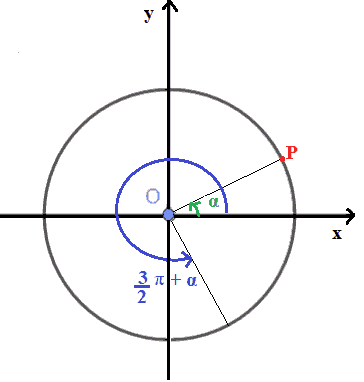
Indichiamo con P1 il punto associato all'angolo orientato (3π/2) + α.
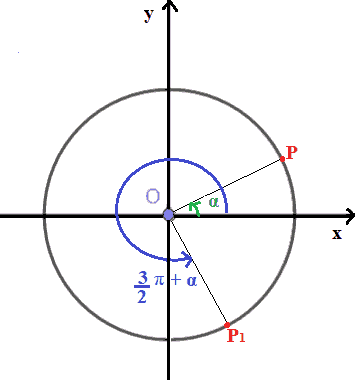
Sappiamo che le coordinate del punto P rappresentano il coseno e il seno di α. Ovvero:
P (cos α ; sen α)
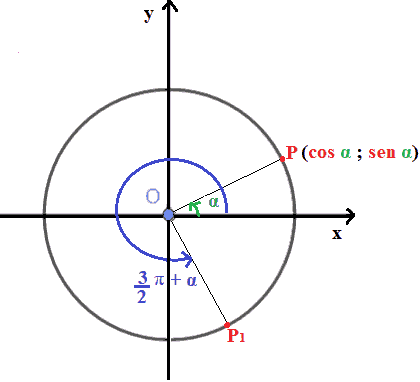
A questo punto andiamo a disegnare il triangolo OHP e il triangolo OH1P1:
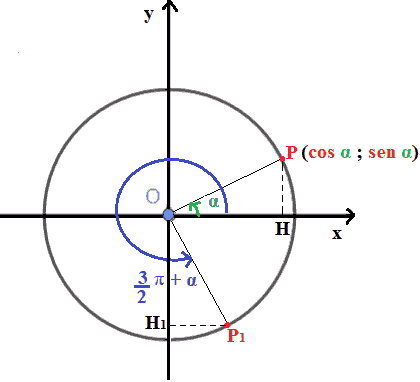
Entrambi i triangoli hanno un
angolo retto: quello con vertice in H
nel triangolo OHP e quello con vertice in H1 nel
triangolo OH1P1.
Possiamo affermare con certezza che si tratta di due angoli retti
poiché essi sono formati da una retta
che interseca perpendicolarmente
l'asse delle x, in un caso, e l'asse delle y, nell'altro.
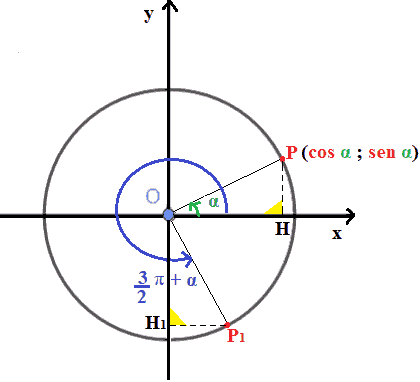
Quindi entrambi i triangoli sono TRIANGOLI RETTANGOLI.
Nei due triangoli sono CONGUENTI:
- l'ipotenusa. Infatti, sia OP che OP1 sono RAGGI della circonferenza goniometrica e quindi, sono pari ad 1;
- un angolo acuto ed esattamente
l'angolo con vertice in O.
Nel triangolo OHP sappiamo, come dato di partenza, che l'angolo con vertice in O è l'angolo α.
Nel triangolo OH1P1 evidentemente l'angolo con vertice in O è l'angolo α dato che lo abbiamo ottenuto sommando all'angolo 3π/2 l'angolo α.
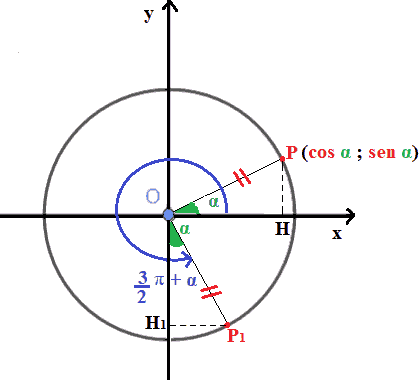
Ma noi sappiamo che due triangoli rettangoli che hanno l'ipotenusa ed un angolo acuto congruenti, sono congruenti.
Quindi possiamo dire che:
- il segmento OH è congruente con il segmento OH1;
- e il segmento HP è congruente con il segmento H1P1;
Sappiamo anche che il segmento OH1 è il SENO dell'angolo (3π/2) + α, mentre il segmento OH è il COSENO dell'angolo α.
Notiamo, però, che il coseno dell'angolo α è positivo, mentre il seno dell'angolo (3π/2) + α è negativo, quindi possiamo dire che
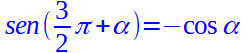
Sappiamo poi che il segmento H1P1 è il COSENO dell'angolo (3π/2) + α, mentre il segmento HP è il SENO dell'angolo α.
In questo caso osserviamo che il seno dell'angolo α e il coseno dell'angolo (3π/2) + α sono entrambi positivi quindi possiamo dire che
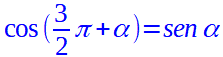
A questo punto non ci resta che ricavare le altre funzioni goniometriche.
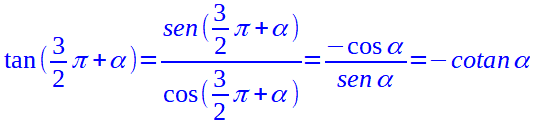
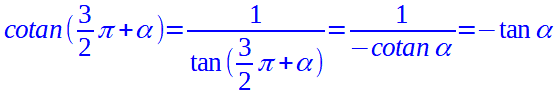
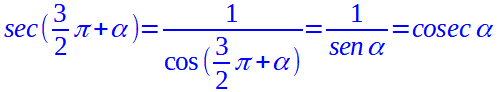
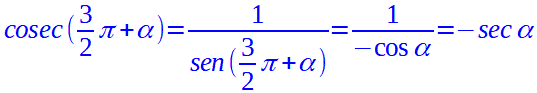
Pertanto, se vogliamo sapere qual è la tangente dell'angolo di 315°, possiamo dire che:
315° = 270° + 45°.
Quindi la tangente dell'angolo di 315° è uguale all'opposto della cotangente dell'angolo di 45° e poiché la cotangente dell'angolo di 45° è pari a 1, possiamo dire che la tangente dell'angolo di 315° è uguale a -1.






