CONGRUENZA E SIMILITUDINE
- Poligoni simili
- Similitudine
- I poligoni
- Figure geometriche equivalenti e figure geometriche congruenti
Nelle lezioni precedenti abbiamo detto che due POLIGONI sono SIMILI se hanno gli ANGOLI CORRISPONDENTI ordinatamente CONGRUENTI e i LATI CORRISPONDENTI PROPORZIONALI.
Sappiamo, inoltre, che due FIGURE GEOMETRICHE si dicono CONGRUENTI quando mediante un movimento rigido è possibile SOVRAPPORRE UNA DI ESSE ALL'ALTRA in modo che esse COINCIDONO.
Disegniamo due poligoni CONGRUENTI:
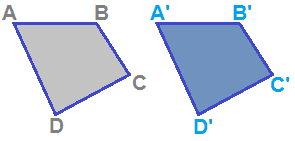
E' evidente che essi sono anche SIMILI poiché hanno gli angoli corrispondenti ordinatamente congruenti e i lati corrispondenti proporzionali. In questo caso il rapporto di similitudine è 1.
Quindi possiamo dire che la CONGRUENZA è un CASO PARTICOLARE di SIMILITUDINE.
Ora disegniamo due poligoni SIMILI:
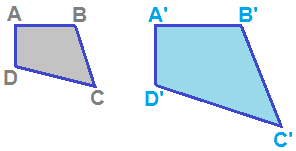
I due poligoni appena disegnati non sono congruenti.
Quindi possiamo affermare che due poligoni CONGRUENTI sono anche SIMILI, ma non vale sempre il contrario.






