TANGENTE
Disegniamo la circonferenza goniometrica e l'angolo orientato α.
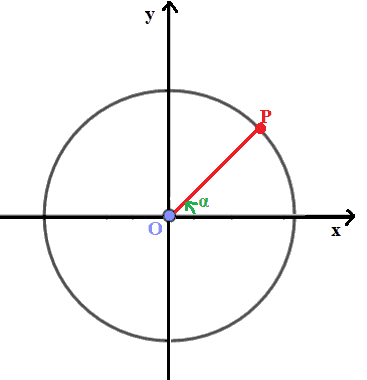
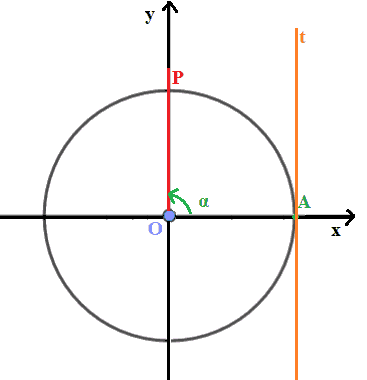
Ora disegniamo una RETTA TANGENTE alla CIRCONFERENZA nel punto A (0 ; 1) e chiamiamo tale retta t.
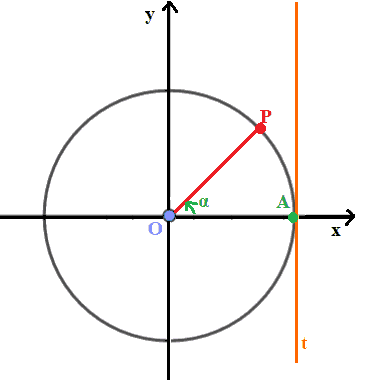
La retta t come si può vedere dall'immagine sopra è PARALLELA all'asse delle y.
Abbiamo indicato con P il punto della circonferenza goniometrica associato all'angolo orientato α.
Ora andiamo ad individuare il punto in cui la retta OP interseca la retta t che abbiamo appena disegnato: chiamiamo questo punto T:
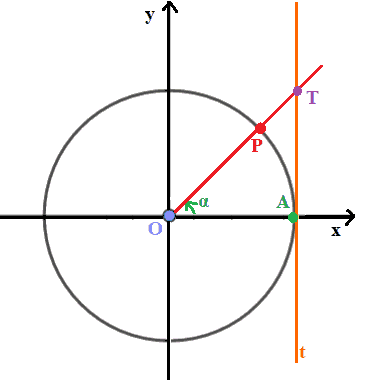
L'ASCISSA del punto T è la stessa del punto A e di tutti i punti della retta t ed esattamente essa è pari ad 1. Inoltre, come si può notare, tale ascissa non dipende dall'ampiezza dell'angolo α.
Invece, l'ORDINATA del punto T dipende dall'ampiezza dell'angolo α.
Vediamolo attraverso un esempio:
- disegniamo sulla circonferenza goniometrica l'angolo orientato β (che si legge beta);
- disegniamo il punto P' (che si legge P primo), cioè il punto della circonferenza goniometrica associato all'angolo orientato β;
- disegniamo la retta t' (che si legge t primo) tangente alla circonferenza nel punto A;
- disegniamo il punto T' (che si legge T primo) cioè il punto in cui la retta OP' interseca la retta t'.
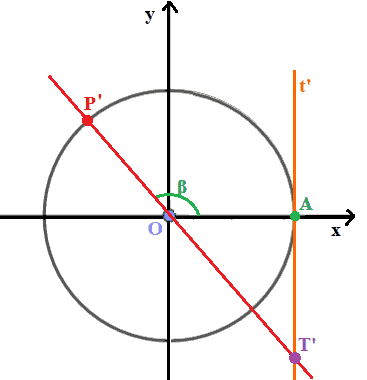
E' evidente che il punto T e il punto T' hanno sempre la stessa ascissa (1) mentre è diversa la loro ordinata.
Si chiama TANGENTE dell'angolo orientato α l'ORDINATA del punto in cui la RETTA TANGENTE alla circonferenza goniometrica nel suo punto di ascissa 1, incontra la retta OP, dove P è il punto associato all'angolo α.
Per indicare la tangente dell'angolo α si usa il simbolo
tan α
oppure
tg α
entrambi si leggono
tangente di alfa.
Quindi possiamo scrivere:
T (1; tan α)
Ora osserviamo cosa accade quando il punto P APPARTIENE all'ASSE delle ORDINATE.
In questo caso la retta OP e la retta t, tangente alla circonferenza goniometrica nel punto A, sono PARALLELE e non si intersecano mai.
Abbiamo detto che questo accade quando il punto P si trova sull'asse delle ordinate, quindi quando esso ha coordinate:
P (0 ; 1)
oppure
P (0 ; -1)
e noi sappiamo che ciò si verifica quando l'angolo α misura 90° e quando misura 270° e tutti i loro multipli.
Esprimendo l'angolo in radianti possiamo dire che ciò si verifica quando l'angolo α misura π/2 e quando misura 3π/2 e tutti i loro multipli.
Quindi, poiché
3π/2 = π/2 + π
Possiamo dire che il valore della TANGENTE di α NON è DEFINITO quando
α = π/2 + kπ
con k ∈ Z
che si legge
con k appartenente all'insieme dei numeri relativi.
Così come abbiamo detto per il seno e per il coseno, anche per la tangente possiamo dire che essa non è espressa da nessuna unità di misura in quanto si tratta di un numero puro o potremmo dire di una grandezza priva di dimensione.
Nella prossima lezione vedremo un altro modo di definire la tangente.






