ARCHI SUPPLEMENTARI
Dallo studio della geometria sappiamo che due ANGOLI si dicono SUPPLEMENTARI quando la loro SOMMA è un ANGOLO PIATTO.
Di conseguenza possiamo dire che l'angolo:
α
e l'angolo
π - α
sono due angoli SUPPLEMENTARI.
Ricordiamo infatti che l'angolo di 180°, espresso in radianti, è uguale a π.
Quindi
π - α + α = π
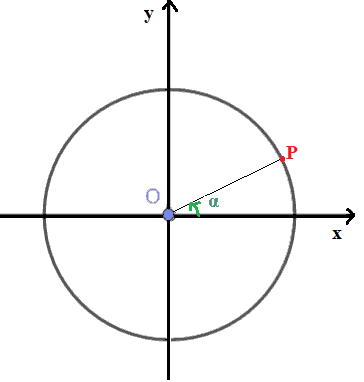
Disegniamo la circonferenza goniometrica e l'angolo orientato α ed indichiamo con P il punto associato a tale angolo.
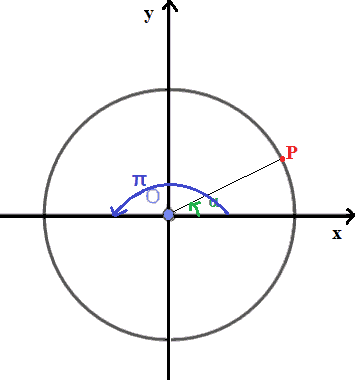
Ora, sulla stessa circonferenza goniometrica, prendiamo l'angolo orientato π
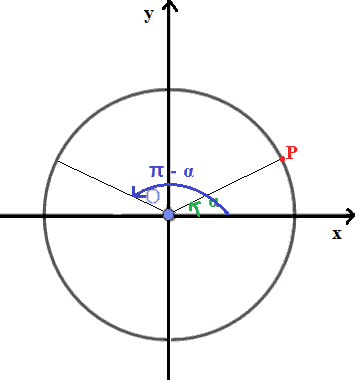
e togliamo da esso l'angolo α in modo da ottenere l'angolo π - α
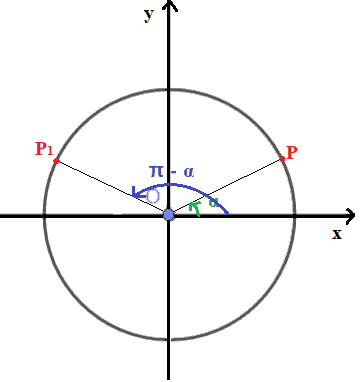
Andiamo ad indicare con P1 (che si legge P con uno) il punto associato all'angolo orientato π - α.
Sappiamo, inoltre, che le coordinate del punto P rappresentano il coseno e il seno di α. Ovvero:
P (cos α ;sen α)
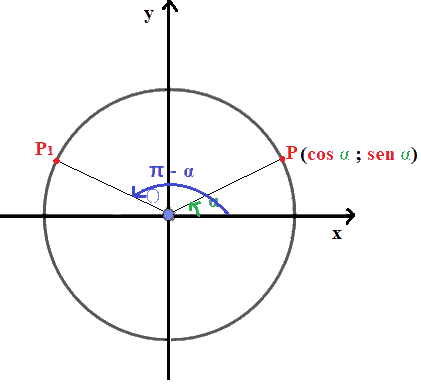
Ora cerchiamo di capire quali sono le coordinate del punto P1.
Disegniamo il triangolo OHP e il triangolo OH1P1:
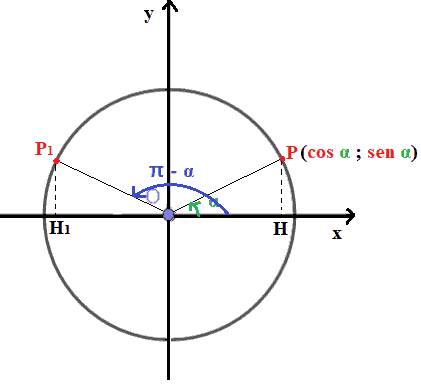
I due triangoli hanno un
angolo retto: quello con vertice in H
nel triangolo OHP e quello con vertice in H1 nel
triangolo OH1P1.
Possiamo affermare con certezza che si tratta di due angoli retti
poiché essi sono formati da due rette
che intersecano perpendicolarmente
l'asse delle x.
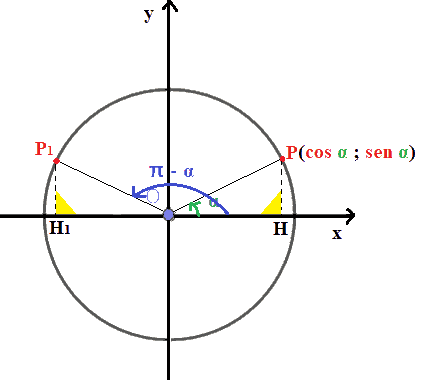
Quindi entrambi sono TRIANGOLI RETTANGOLI.
Nei due triangoli sono CONGUENTI:
- l'ipotenusa, infatti, sia OP che OP1 sono RAGGI della circonferenza goniometrica e quindi, sono pari ad 1;
- un angolo acuto ed esattamente
l'angolo con vertice in O.
Nel triangolo OHP sappiamo, come dato di partenza, che l'angolo con vertice in O è l'angolo α.
Nel triangolo OH1P1 evidentemente l'angolo con vertice in O è l'angolo α dato che lo abbiamo ottenuto da π - α.
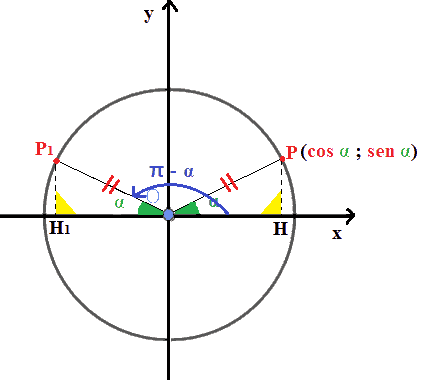
Ma noi sappiamo che due triangoli rettangoli che hanno l'ipotenusa ed un angolo acuto congruenti, sono congruenti.
Quindi possiamo dire che:
- il segmento OH è congruente con il segmento OH1;
- e il segmento HP è congruente con il segmento H1P1;
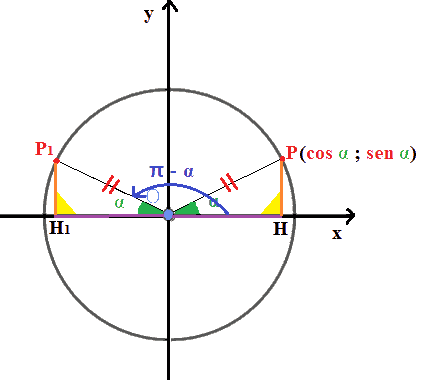
Ma noi sappiamo che il segmento OH1 è il COSENO dell'angolo π - α, mentre il segmento OH è il COSENO dell'angolo α.
Osserviamo però che, poiché l'angolo α si trova nel primo quadrante, il suo coseno è positivo, mentre l'angolo π - α si trova nel secondo quadrante e quindi il suo coseno è negativo.
Quindi possiamo dire che il COSENO dell'angolo π - α è uguale all'opposto del COSENO dell'angolo α. Ovvero:
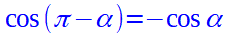
Sappiamo poi che il segmento H1P1 è il SENO dell'angolo π - α, mentre il segmento HP è il SENO dell'angolo α.
Inoltre l'angolo α si trova nel primo quadrante e, di conseguenza, il suo seno è positivo. L'angolo π - α si trova nel secondo quadrante e quindi anche il suo seno è positivo.
Quindi possiamo dire che il SENO dell'angolo π - α è uguale al SENO dell'angolo α. Ovvero:
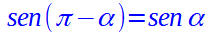
Dalle due funzioni goniometriche fondamentali, come abbiamo visto anche nelle lezioni precedenti, possiamo ricavare le altre.
Quindi:
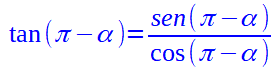
Ma poiché abbiamo appena visto che:
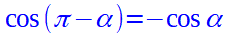
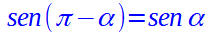
La tangente dell'angolo π - α diventa:
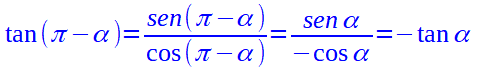
Procedendo allo stesso modo possiamo dire che:
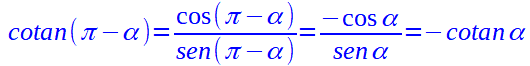

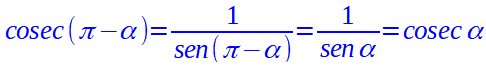
Così, ad esempio, se abbiamo un angolo di 135° e vogliamo conoscere il suo seno, possiamo scrivere:
135° = 180° - 45°
quindi il seno dell'angolo di 135° è uguale al seno dell'angolo di 45° e poiché il seno dell'angolo di 45° è pari a radice di due fratto due, questo è anche il seno dell'angolo di 135°.






