ANGOLI COMPLEMENTARI, SUPPLEMENTARI ED ESPLEMENTARI
Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:
- Gli angoli
- Somma di due angoli
- Angolo piatto, angolo giro e angolo nullo
- Angolo retto - angolo acuto - angolo ottuso
Consideriamo due angoli, l'angolo Alfa e l'angolo Beta:
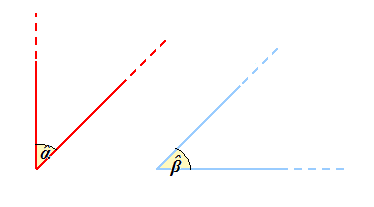
Ora sommiamo i due angoli e avremo:
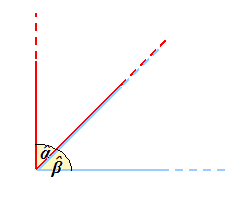
Come possiamo osservare la SOMMA dei due angoli dati è un ANGOLO RETTO.
I due angoli Alfa e Beta si dicono, in questo caso, ANGOLI COMPLEMENTARI.
Consideriamo ora i seguenti angoli:
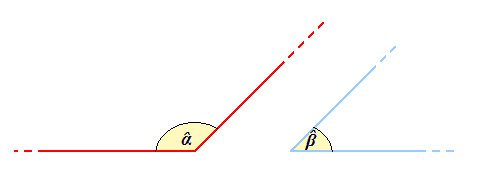
Ora sommiamo i due angoli e avremo:
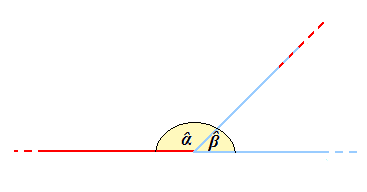
Come possiamo osservare la SOMMA dei due angoli è un ANGOLO PIATTO.
I due angoli Alfa e Beta si dicono, in questo caso, ANGOLI SUPPLEMENTARI.
Infine consideriamo i seguenti angoli:
Ora sommiamo i due angoli e avremo:
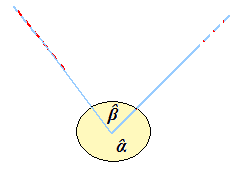
Come possiamo osservare la SOMMA dei due angoli è un ANGOLO GIRO.
I due angoli Alfa e Beta si dicono, per questa ragione, ANGOLI ESPLEMENTARI.
Ricapitolando:
- due ANGOLI si dicono COMPLEMENTARI se la loro SOMMA è un ANGOLO RETTO;
- due ANGOLI si dicono SUPPLEMENTARI se la loro SOMMA è un ANGOLO PIATTO;
- due ANGOLI si dicono ESPLEMENTARI se la loro SOMMA è un ANGOLO GIRO.
