ANGOLI NOTEVOLI: L'ANGOLO DI 45°
Continuiamo a vedere come possiamo calcolare i valori delle funzioni goniometriche nel caso degli ANGOLI NOTEVOLI ed occupiamoci dell'angolo di 45°, ovvero dell'angolo di π/4 RADIANTI.
Costruiamo il triangolo PHO:
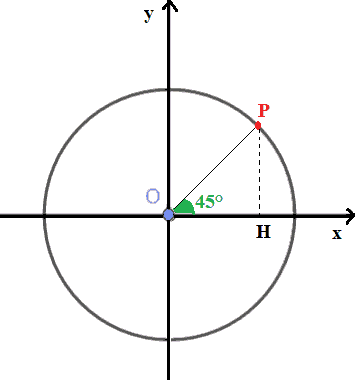
L'angolo con vertice in H è un angolo retto essondo il segmento PH perpendicolare all'asse delle ascisse.
Il triangolo è, quindi, un TRIANGOLO RETTANGOLO.
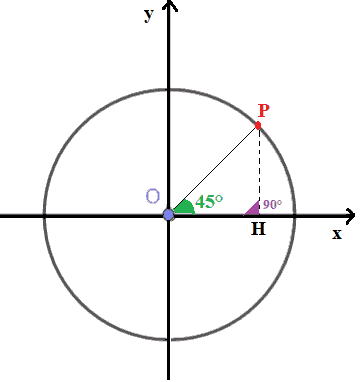
Noi conosciamo la misura dell'angolo con vertice in O, che ha um'ampiezza di 45°, e la misura dell'angolo con vertice in H che, essendo retto, misura 90°. Poiché la somma degli angoli interni di un triangolo è sempre pari a 180°, possiamo dire con certezza che l'angolo con vertice in P misura 45° (infatti 180° - 45° - 90° = 45°).
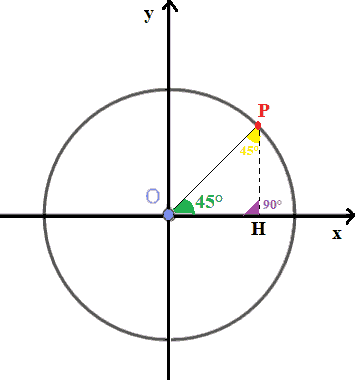
Quindi possiamo dire che il triangolo PHO è un TRIANGOLO ISOSCELE RETTANGOLO avendo due angoli della stessa ampiezza ed una angolo retto: quindi i lati PH e OH sono CONGRUENTI essendo i due lati obbliqui del triangolo isoscele. Al tempo stesso essi rappresentano anche i due CATETI del triangolo rettangolo.
Inoltre sappiamo che il lato OP, essendo il raggio della circonferenza goniometrica, è pari ad 1.
Applicando il teorema di Pitagora possiamo scrivere:
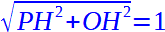
Poiché i lati PH e OH hanno la stessa lunghezza possiamo scrivere:
PH = OH
e quindi:
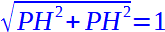
da cui andiamo a ricavare il valore di PH:

Portiamo PH2 fuori dalla radice quadrata:

Dividiamo primo e secondo membro per la radice di 2:
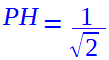
Moltiplichiamo numeratore e denominatore per radice di 2:
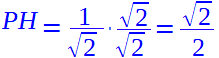
Ma noi sappiamo che PH è il SENO dell'angolo di 45°: quindi possiamo scrivere
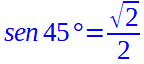
Occupiamoci ora del coseno.
Il coseno è pari al segmento OH. Ma noi sappiamo che esso è lungo esattamente come il segmento PH, quindi anche il coseno è uguale a:
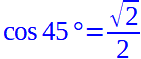
A questo punto possiamo calcolare la tangente nel modo seguente:
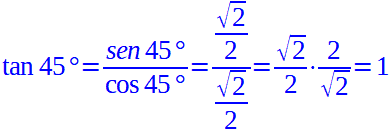
Chiaramente la cotangente sarà:
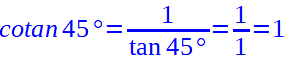
Andiamo a calcolare anche la secante:
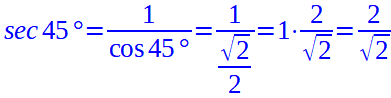
Eliminiamo la radice dal denominatore della frazione moltiplicando numeratore e denominatore per la radice di due ed otteniamo:
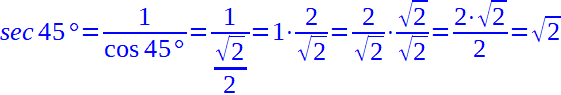
A questo punto non rimane che andare a calcolare la cosecante:
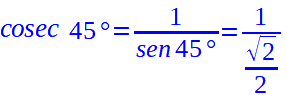
Chiaramente il risultato sarà lo stesso della secante:
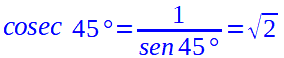
Nella prossima lezione continueremo a vedere i valori delle funzioni goniometriche di angoli notevoli.






