TRIANGOLO ISOSCELE
- Triangoli
- Elementi del triangolo
- Caratteristiche dei triangoli
- Classificazione dei triangoli
- Figure geometriche equivalenti e figure geometriche congruenti
Nella lezione precedente abbiamo visto che un TRIANGOLO si dice ISOSCELE se esso ha DUE LATI CONGRUENTI, cioè aventi la stessa lunghezza:
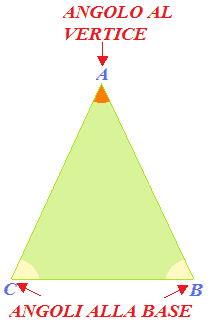
Ora osserviamo meglio questo triangolo, che chiamiamo ABC:
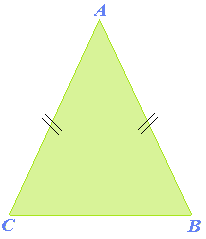
Due lati del triangolo hanno la stessa lunghezza, ed esattamente i lati AB e AC. Essi si dicono semplicemente LATI del triangolo o anche LATI OBLIQUI, mentre il BC si chiama BASE del triangolo.
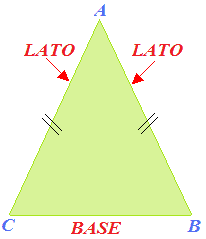
L'angolo 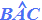 è
FORMATO dai DUE
LATI UGUALI. Esso prende il nome di ANGOLO
AL VERTICE.
è
FORMATO dai DUE
LATI UGUALI. Esso prende il nome di ANGOLO
AL VERTICE.
Mentre gli altri due angoli sono detti ANGOLI ALLA BASE.
Ora disegniamo su un foglio di carta
trasparente un angolo 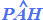
Ora, con un compasso, facciamo CENTRO nel vertice A e, scegliendo un raggio a piacere, descriviamo una CIRCONFERENZA:

La circonferenza appena disegnata interseca i segmenti AH e AP rispettivamente nei punti B e C:
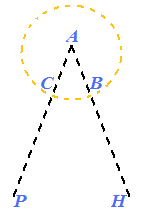
Ora congiungiamo i punti B e C. Otterremo il triangolo ABC:
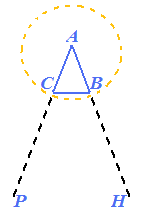
Ora pieghiamo a metà il nostro foglio in maniera tale che il punto B coincida con il punto C:
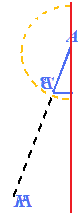
Con la linea rossa abbiamo indicato il punto in cui il foglio risulta piegato a metà.
Ora noteremo che, non solo i lati AB
e AC sono congrui, ma
che anche gli angoli alla base del triangolo  e
e 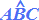 sono congrui.
sono congrui.
Possiamo, allora, affermare che gli ANGOLI ALLA BASE di un TRIANGOLO ISOSCELE sono CONGRUENTI.
Quindi il TRIANGOLO ISOSCELE ha sempre DUE LATI e DUE ANGOLI CONGRUENTI.






