IPERBOLE EQUILATERA RIFERITA AI SUOI ASINTOTI
- L'iperbole
- Equazione dell'iperbole
- Elementi dell'iperbole
- Asintoti dell'iperbole
- Eccentricità dell'iperbole
- Iperbole con fuochi sull'asse delle y
- Elementi dell'iperbole con fuochi sull'asse delle y
- Iperbole equilatera riferita agli assi
- Fuochi, vertici e asintoti dell'iperbole
- Assi cartesiani ortogonali
- Figure geometriche equivalenti e figure geometriche congruenti
- Teorema di Pitagora: dimostrazione
- Le formule del teorema di Pitagora
- Le formule inverse del teorema di Pitagora
Nella lezione precedente abbiamo parlato dell'IPERBOLE EQUILATERA con CENTRO nell'ORIGINE degli ASSI e riferita agli ASSI CARTESIANI.
Esiste, però, anche un'altra IPERBOLE EQUILATERA, che ha il CENTRO sempre nell'ORIGINE degli ASSI, ma è riferita ai suoi ASINTOTI.
Essa si può presentare in uno dei due modi che seguono:
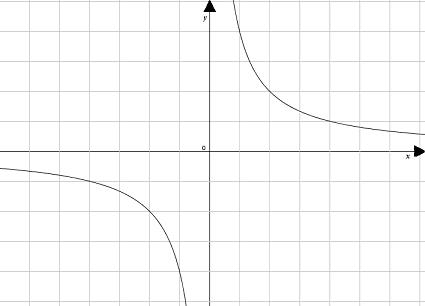
- l'iperbole è situata nel PRIMO
e TERZO quadrante
- l'iperbole è situata nel SECONDO
e QUARTO quadrante
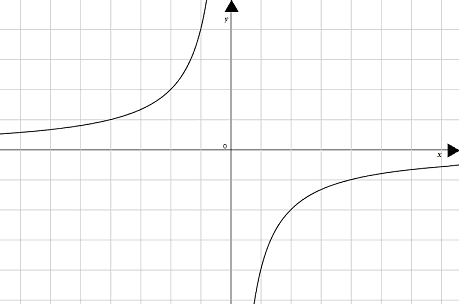
Questo tipo di iperbole ha, esattamente come l'iperbole equilatera riferita agli assi, il SEMIASSE TRAVERSO UGUALE al SEMIASSE NON TRAVERSO, cioè:
a = b.
L'IPERBOLE EQUILATERA riferita agli ASINTOTI ha:
- il CENTRO nell'origine degli assi (come l'iperbole equilatera riferita agli assi);
- gli ASSI CARTESIANI come ASINTOTI;
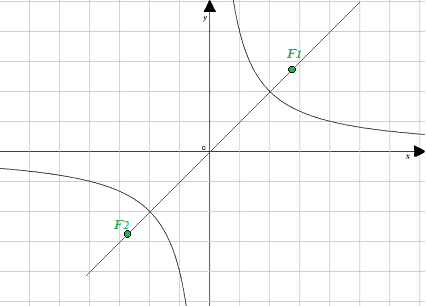
- i FUOCHI situati o sulla
BISETTRICE
del PRIMO e del TERZO QUADRANTE oppure sulla BISETTRICE del SECONDO e
del QUARTO QUADRANTE
Le due iperboli appena viste si dicono anche IPERBOLE EQUILATERA RUOTATA di 45° (in senso orario nel primo caso e antiorario nel secondo) in quanto ottenute dall'iperbole equilatera riferita agli assi attraverso una rotazione.
Vediamo ora qual è l'equazione di questa curva. Partiamo dal caso in cui i FUOCHI sono situati sulla BISETTRICE del PRIMO e TERZO QUADRANTE. Ovviamente anche i VERTICI sono situati su tale bisettrice come si può vedere dall'immagine sotto:
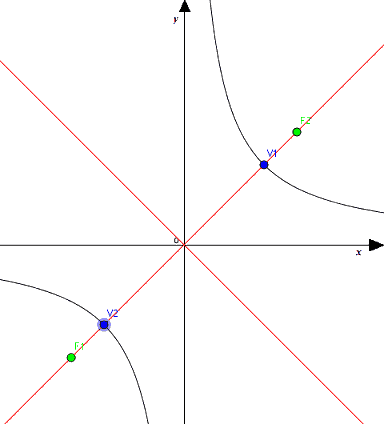
Questa iperbole nasce dalla rotazione in senso antiorario della iperbole equilatera riferita agli assi che nell'immagine sottostante abbiamo disegnato in viola:
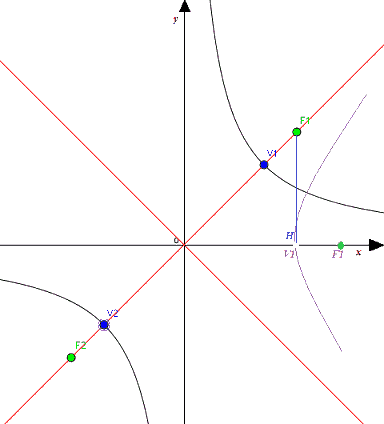
Sappiamo, quindi che:
V1 (a; 0)
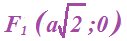
Ora, il segmento OV1 sarà congruente con il segmento OV1 e di conseguenza sarà pari ad a. Quindi:
OV1 = a.
Il segmento OF1 sarà congruente con il segmento OF1 e di conseguenza sarà pari ad a per radice di 2. Quindi:
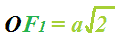
Come si può notare il segmento OH è congruente con il segmento F1H. E, poiché il segmento OH non è altro che il semiasse traverso dell'iperbole viola, esso è pari ad a. Quindi possiamo scrivere:
OH = F1H = a.
Possiamo giungere a questo risultato anche applicando il teorema di Pitagora: infatti il segmento F1H è uno dei cateti del triangolo OF1H. Quindi possiamo scrivere
F1H2 = OF12 - OV12
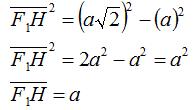
Questo significa che l'ascisse del punto F1 è a. Poiché tale punto si trova sulla bisettrice del primo e del terzo quadrante, anche l'ordinata del punto F1 è a. Quindi possiamo scrivere:
F1 (a; a)
e di conseguenza
F2 (-a; -a)
Applichiamo ora la definizione di iperbole. Un punto P (x; y) appartiene all'iperbole se:
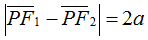
Sostituiamo le coordinate di F1 e F2 e risolviamo:
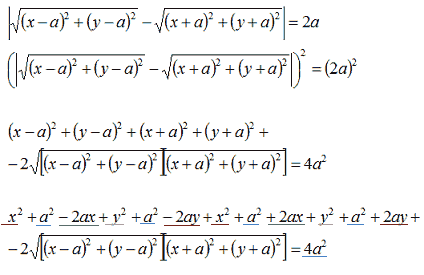

Ora poniamo
a2/2 = k
e scriviamo l'EQUAZIONE dell'IPERBOLE EQUILATERA riferita ai suoi ASINTOTI nel modo seguente
xy = k.
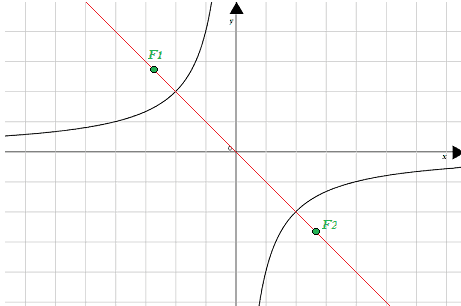
Se noi avessimo ruotato l'iperbole in modo da averla nel secondo e nel quarto quadrante, i fuochi avrebbero avuto come coordinate
F1 (-a; a)
e
F2 (a; -a)
e attraverso i vari passaggi visti, avremmo trovato che l'equazione dell'iperbole è:
xy = -(a2/2) = -k.
Quindi possiamo dire che l'equazione
xy = ±k
è l'equazione dell'iperbole equilatera riferita ai suoi asintoti e il valore di k sarà positivo o negativo a seconda dei quadranti nei quali sono collocati i rami dell'iperbole.
Nella prossima lezione continueremo l'esame di tale iperbole.






