ECCENTRICITA' DELL'IPERBOLE
In questa lezione vedremo cosa si indente per ECCENTRICITA' DELL'IPERBOLE.
Si definisce ECCENTRICITA'dell'IPERBOLE il RAPPORTO tra la SEMIDISTANZA FOCALE e il SEMIASSE TRAVERSO.
Tale rapporto viene indicato con la lettera e minuscola. Quindi:
e = semidistanza focale / semiasse traverso.
Ora, nel caso dell'IPERBOLE con i FUOCHI sull'ASSE DELLE ASCISSE e CENTRO DI SIMMETRIA nell'ORIGINE DEGLI ASSI, sappiamo che la distanza focale è uguale a 2c, mentre l'asse traverso è uguale a 2a. Quindi:
distanza focale = 2c
semidistanza focale = c
asse traverso = 2a
semiasse traverso = a.
Pertanto
e = c/ a.
Nello scrivere l'equazione dell'iperbole abbiamo posto:
b2 = c2 - a2.
Quindi, noi sappiamo che
c2 > a2
e di conseguenza:
c > a.
Questo significa che l'ECCENTRICITA' dell'IPERBOLE assume sempre VALORI MAGGIORI di 1, ovvero:
e > 1.
Quando l'ECCENTRICITA' dell'IPERBOLE si avvicina ad 1, l'iperbole appare molto SCHIACCIATA sull'ASSE DELLE ASCISSE.
Esempio:
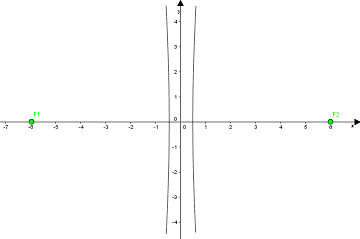
esaminiamo l'iperbole
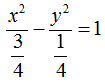
Ora vogliamo trovare l'eccentricità dell'iperbole.
Noi sappiamo che
a2 = 3/4
quindi
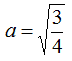
Non conosciamo il valore di c, ma sappiamo che
b2 = 1/4
e che la relazione che lega a, b e c è la seguente
b2 = c2 - a2.
Quindi
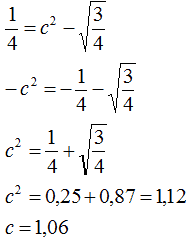
A questo punto troviamo il valore di e:
e =c/ a = 1,06/ (3/4) = 1,06/ 0,75 = 1,41.
Disegnando l'iperbole notiamo che essa è piuttosto schiacciata sull'asse delle ascisse:
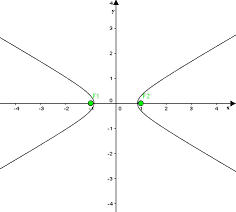
Invece, quando l'ECCENTRICITA' si allontana maggiormente da 1 assumendo valori più elevati, l'iperbole appare molto SCHIACCIATA sull'ASSE DELLE ORDINATE.
Esempio:
esaminiamo l'iperbole
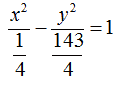
Ora vogliamo trovare l'eccentricità dell'iperbole.
Noi sappiamo che
a2 = 1/4
quindi
a = 1/2.
Non conosciamo il valore di c, ma sappiamo che
b2 = 143/4
e che la relazione che lega a, b e c è la seguente
b2 = c2 - a2.
Quindi
143/4 = c2 - 1/4
-c2 = -143/4 - 1/4
c2 = 143/4 + 1/4
c2 = 144 /4 = 36
c = 6.
A questo punto troviamo il valore di e:
e =c/ a = 6/ (1/2) = 6 · 2 = 12.
Disegnando l'iperbole notiamo che essa è maggiormente schiacciata sull'asse delle ordinate rispetto al caso precedente: