TEOREMA DI PITAGORA: DIMOSTRAZIONE

Pubblicità/Advertising

Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:

• Triangolo rettangolo
• Quadrato
• Figure geometriche equivalenti e figure geometriche congruenti

Disegniamo su un cartoncino, di spessore costante, un TRIANGOLO RETTANGOLO:

Ora, sempre usando lo stesso cartoncino, costruiamo TRE QUADRATI che chiamiamo rispettivamente Q₁, Q₂, Q₃ aventi come LATI rispettivamente l'ipotenusa AB e i due cateti AC e CB:

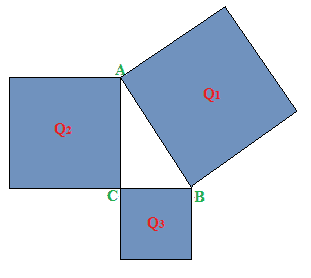
Ora ritagliamo i tre quadrati Q₁, Q₂, Q₃ e li PESIAMO su una bilancia di precisione.

Noteremo che il peso complessivo dei due quadrati Q₂ e Q₃ è uguale al PESO del quadrato Q₁.

Ma se il peso complessivo di Q₂ e Q₃ è uguale al peso del quadrato Q₁ evidentemente Q₂ e Q₃ insieme hanno la stessa ESTENSIONE di Q₁.

Inoltre possiamo verificare che quanto detto è vero per qualsiasi triangolo rettangolo da noi disegnato.

Possiamo allora affermare che in OGNI TRIANGOLO RETTANGOLO, il QUADRATO costruito sull'IPOTENUSA è EQUIVALENTE alla SOMMA dei QUADRATI costruiti sui DUE CATETI.

Nella prossima lezione vedremo un altro metodo per dimostrare il TEOREMA DI PITAGORA.

Lezione successiva

Indice degli argomenti sul teorema di Pitagora

Pubblicità/Advertising