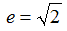IPERBOLE EQUILATERA RIFERITA AGLI ASSI
- L'iperbole
- Equazione dell'iperbole
- Elementi dell'iperbole
- Asintoti dell'iperbole
- Eccentricità dell'iperbole
- Iperbole con fuochi sull'asse delle y
- Elementi dell'iperbole con fuochi sull'asse delle y
- Fuochi, vertici e asintoti dell'iperbole
- Assi cartesiani ortogonali
- Bisettrice del primo e terzo quadrante
- Bisettrice del secondo e quarto quadrante
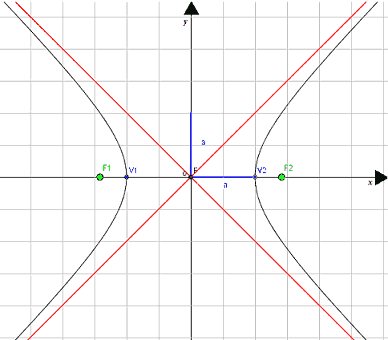
Immaginiamo di avere un'iperbole con CENTRO nell'ORIGINE degli ASSI e con SEMIASSE TRAVERSO UGUALE al SEMIASSE NON TRAVERSO. In altre parole si avrà:
a = b.
Graficamente l'iperbole si presenta così:
Poiché
a = b
l'equazione dell'iperbole diventa
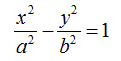
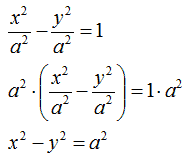
Quindi, possiamo dire che
x2 - y2 = a2
è l'equazione dell'IPERBOLE EQUILATERA riferita al CENTRO e agli ASSI CARTESIANI e avente i FUOCHI sull'ASSE delle ASCISSE.
I FUOCHI dell'IPERBOLE EQUILATERA, sono
F1 (-c; 0) F2 (c; 0).
Essendo la relazione che lega c con a e b, la seguente:
c2 = a2 + b2
e poiché nell'iperbole equilatera
a = b
possiamo scrivere
c2 = a2 + a2 = 2a2
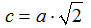
I vertici sono
V1 (-a; 0)
V2 (a; 0).
I vertici non reali sono
V3 (0; -b)
V4 (0; b)
ma poiché
a = b
essi diventano
V3 (0; -a)
V4 (0; a).
Passiamo agli ASINTOTI. Essendo essi:
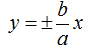
e poiché nell'iperbole equilatera
a = b
possiamo scrivere
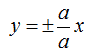
ovvero
y = ± x.
In altre parole, gli asintoti non sono altro che la BISETTRICE del PRIMO e TERZO QUADRANTE e la BISETTRICE del SECONDO e QUARTO QUADRANTE come possiamo anche notare dal grafico precedente.
Infine, l'eccentricità è data sempre da
e = c/a
ma poiché
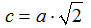
possiamo dire che
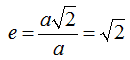
Ovviamente, anche l'IPERBOLE EQUILATERA può avere i FUOCHI sull'ASSE delle ORDINATE.
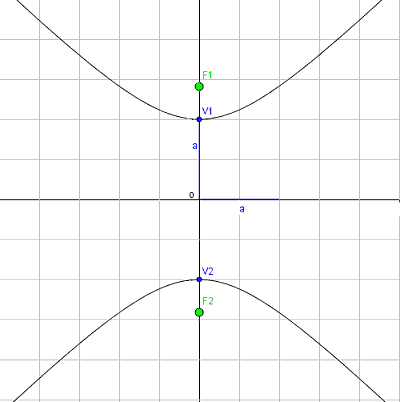
Sarà facile dimostrare che questa iperbole ha:
- equazione
x2 - y2 = - a2
- fuochi
F1 (0; -c) F2 (0; c)
-
relazione che
lega c
con a
e b
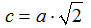
- vertici
V1 (0; -a)
V2 (0; a).
- vertici non reali
V3 (-a; 0)
V4 (a; 0)
- asintotitoy
= ± x
- eccentricità