LE FORMULE INVERSE DEL TEOREMA DI PITAGORA
- Teorema di Pitagora: dimostrazione
- Teorema di Pitagora: dimostrazione
- Le formule del teorema di Pitagora
- Esempi di applicazione del teorema di Pitagora
- Triangolo rettangolo
Nelle lezioni precedenti abbiamo visto come è possibile applicare il TEOREMA DI PITAGORA per trovare la misura dell'ipotenusa di un triangolo rettangolo conoscendo la misura dei suoi cateti.
Ora vogliamo vedere come è possibile trovare la misura di un cateto del triangolo rettangolo se conosciamo la misura dell'altro cateto e quella dell'ipotenusa.
Abbiamo visto che
i2 = c12 + c22
dove
i = ipotenusa
c1 = un cateto
c2 = l'altro cateto.
Supponiamo di voler trovare la misura del cateto c1. Essa sarà data da:
c12 = i2 - c22.
Ed estraendo la radice quadrata si avrà:
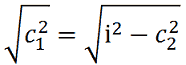
da cui avremo:
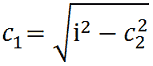
Allo stesso modo se vogliamo trovare la misura del cateto c2. Essa sarà data da:
c22 = i2 - c12.
Quindi
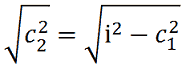
da cui avremo:
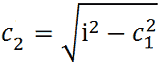
Nella prossima lezione vedremo come applicare praticamente queste formule.






