EQUAZIONE DELL'IPERBOLE

Pubblicità/Advertising

Per comprendere meglio questo argomento, leggi prima le seguenti lezioni:

• L'iperbole
• Punto medio di un segmento
• La retta
• Distanza tra due punti sul piano cartesiano
• Caratteristiche dei triangoli
• L'insieme dei numeri reali
• Simboli usati per l'insieme dei numeri reali
• Radice quadrata
• Raccoglimento a fattor comune parziale

Dopo aver visto, nella lezione precedente, cosa si intende per IPERBOLE, vediamo qual è la sua EQUAZIONE.

Per semplificare le cose disegniamo un'IPERBOLE nella quale:

• l'ORIGINE degli ASSI è anche il PUNTO MEDIO dei FUOCHI;
• l'ASSE delle ASCISSE è la RETTA CHE CONGIUNGE i FUOCHI.

Ipotizziamo che i due fuochi abbiano le seguenti coordinate:

F₁ (-c; 0)

F₂ (c; 0).

Supponiamo, inoltre, che il generico punto P appartenente all'iperbole abbia coordinate

P (x; y).

Noi sappiamo che, affinché P sia un punto dell'IPERBOLE, si deve verificare la condizione:

| PF₁ -PF₂ | = 2a.

Ricordiamo che la distanza tra due punti è:

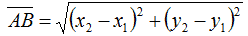
Sostituendo le coordinate dei punti P e F₁ possiamo dire che la distanza PF₁ è data da:

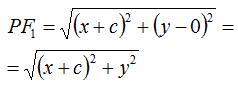
Sostituendo le coordinate dei punti P e F₂ possiamo dire che la distanza PF₂ è data da:

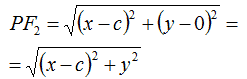
Quindi, la condizione

| PF₁ -PF₂ | = 2a

può essere scritta nel modo seguente

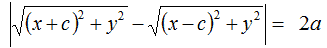
che equivale a scrivere

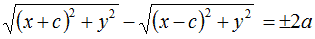
Isoliamo la prima radice a primo membro, portando la seconda radice a secondo membro e cambiandole di segno:

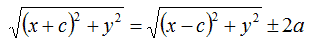
Eleviamo al quadrato primo e secondo membro ed otteniamo:

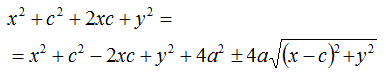
Osserviamo che ±2a elevato al quadrato, diventa +4a² dato che un numero sia esso positivo che negativo, elevato al quadrato, diventa sempre positivo.

Semplifichiamo:

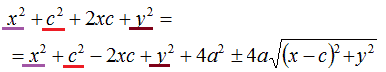
ed otteniamo

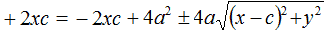
Ora isoliamo la radice a secondo membro:

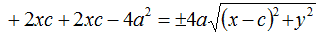
e sommiamo i termini simili:

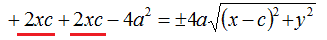
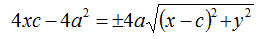
Dividiamo primo e secondo membro per 4:

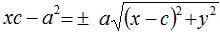
Eleviamo, ancora, primo e secondo membro al quadrato:

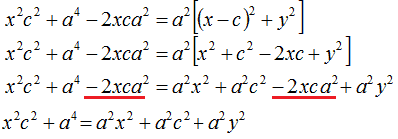
Anche in questo caso, quando eleviamo ± a al quadrato otteniamo un numero positivo.

Ora ordiniamo un po' i nostri valori:

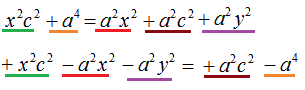
Tra i primi due termini del primo membro mettiamo in evidenza la x², mentre a secondo membro mettiamo in evidenza a². Avremo:

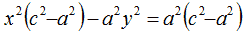
Ora poniamo

b² = c² - a².

Tale sostituzione è possibile perché esiste sempre un valore di b appartenente all'insieme dei reali positivi R⁺

tale che

c² - a² = b² .

Vediamone il perché:

Disegniamo il punto P appartenente all'iperbole e i fuochi F₁ e F₂:

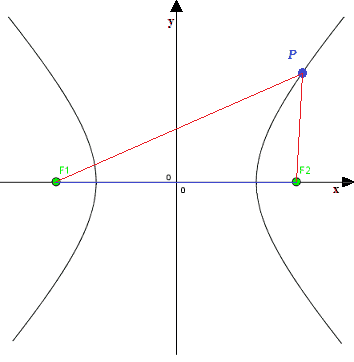
I segmenti PF₁, PF₂, F₁F₂ sono i lati di un TRIANGOLO.

Indichiamo la lunghezza del segmento F₁F₂ con 2c, ovvero

F₁F₂ = 2c.

Ora, noi sappiamo che in un TRIANGOLO OGNI LATO è sempre MAGGIORE della DIFFERENZA DEGLI ALTRI DUE.

Quindi possiamo scrivere:

F₁F₂ > | PF₁ -PF₂ |.

Ma poiché

F₁F₂ = 2c

e

| PF₁ -PF₂ | = 2a

possiamo dire che

2c > 2a

ovvero

c > a

quindi

c² > a²

da cui

c² - a² > 0.

Quindi ci sarà sempre un valore di b appartenente all'insieme dei reali positivi R⁺ tale che

c² - a² = b² .

Ora, torniamo alla nostra equazione, ed effettuiamo la sostituzione detta. Avremo:

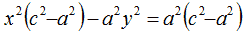
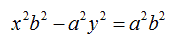
Dividiamo entrambi i membri per a² b² in modo da avere:

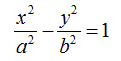
Quella che abbiamo scritto è l'EQUAZIONE dell'IPERBOLE con i FUOCHI sull'ASSE DELLE ASCISSE.

Lezione precedente - Lezione successiva

Indice degli argomenti sull'iperbole

Pubblicità/Advertising