ASINTOTI DELL'IPERBOLE
- L'iperbole
- Equazione dell'iperbole
- Elementi dell'iperbole
- La retta
- Retta passante per l'origine degli assi
- Coefficiente angolare
- Equazione della circonferenza con centro nell'origine degli assi
- Rette perpendicolari
- Retta parallela all'asse delle y
- Triangoli
- Le formule del teorema di Pitagora
- Triangolo rettangolo
Nella lezione precedente abbiamo visto che
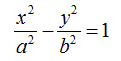
è l'EQUAZIONE dell'IPERBOLE con iFUOCHI sull'ASSE DELLE ASCISSE e CENTRO DI SIMMETRIA nell'ORIGINE degli ASSI.
Graficamente avremo:
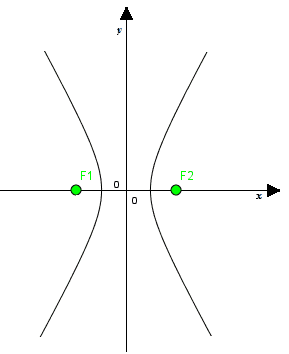
Inoltre abbiamo visto alcuni degli elementi dell'iperbole: distanza focale, vertici, asse traverso, asse non traverso, centro di simmetria.
In questa lezione ci occuperemo degli ASINTOTI.
Osserviamo che, mano a mano che ci allontaniamo dai fuochi, la curvatura dell'iperbole si riduce ed essa assume un andamento quasi rettilineo.
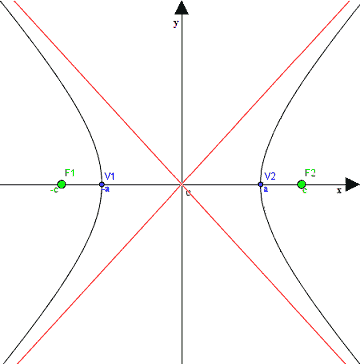
Prendono il nome di ASINTOTI delle rette alle quali l'IPERBOLE tende ad avvicinarsi senza toccarle mai.
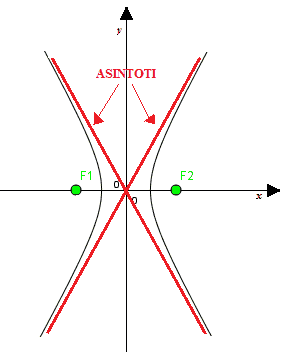
Notiamo che l'IPERBOLE ha DUE ASINTOTI.
Inoltre, è evidente che gli ASINTOTI dell'iperbole canonica passano per il CENTRO di SIMMETRIA dell'iperbole, cioè per l'origine degli assi.
Poniamoci, ora, il problema di capire come possiamo determinare l'equazione dei due ASINTOTI.
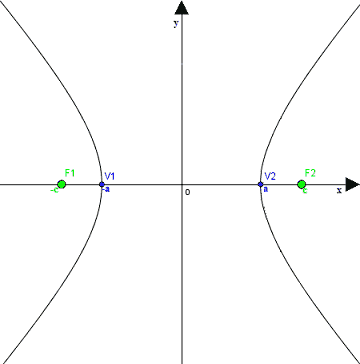
Disegniamo un'IPERBOLE i cui fuochi siano
F1 (-c; 0)
F2 (c; 0)
e i cui vertici siano:
V1 (-a; 0)
V2 (a; 0).
Ora, tracciamo sul grafico i due ASINTOTI:
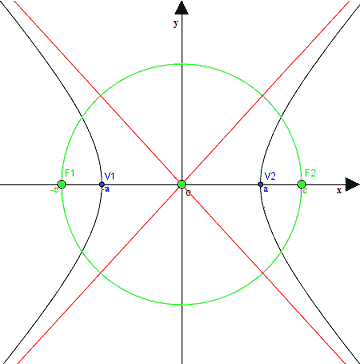
Ora disegniamo anche una CIRCONFERENZA con:
- centro nell'ORIGINE DEGLI ASSI;
- RAGGIO
r = c
ovvero il raggio è pari alla semidistanza focale.
L'EQUAZIONE della CIRCONFERENZA con CENTRO nell'ORIGINE degli ASSI è
x2 + y2 = r2.
Quindi, poiché nel nostro caso
r = c
l'equazione della nostra circonferenza è
x2 + y2 = c2.
Ora disegniamo la RETTA PERPENDICOLARE all'ASSE delle x e passante per il VERTICE V2 dell'IPERBOLE:
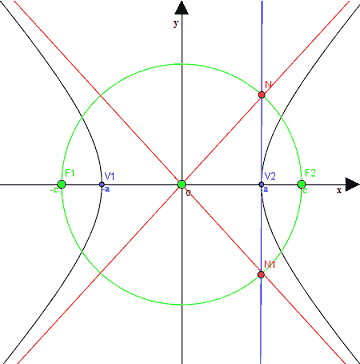
La retta appena disegnata interseca la circonferenza nei punto N e N1.
Ora osserviamo il TRIANGOLO OV2N:
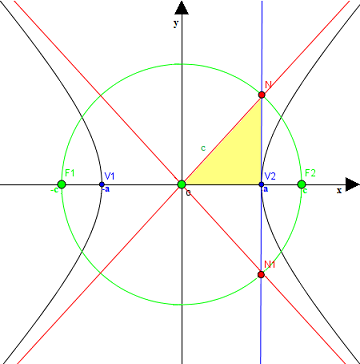
Noi conosciamo la misura di due dei lati:
- il lato OV2 pari ad a;
- il lato O N che non è altro che il raggio della circonferenza e, quindi, è pari a c.
Trattandosi di un triangolo rettangolo possiamo trovare la misura del terzo lato, V2N, applicando il TEOREMA DI PITAGORA:
(V2N)2 = c2 - a2.
Ma noi sappiamo che:
b2 = c2 - a2
quindi possiamo dire che
(V2N)2 = c2 - a2= b2
(V2N)2 = c2 - a2 = b2
V2N= b.
Quindi, il punto N ha come coordinate
N (a; b)
di conseguenza il punto N1 ha come coordinate
N1 (a; -b).
Ora possiamo dire che un asintoto passa:
- per l'origine degli assi;
e
- per il punto N (a; b).
L'altro asintoto passa:
- per l'origine degli assi;
e
- per il punto N1 (a; -b).
Abbiamo detto che gli ASINTOTI passano per l'origine degli assi e sappiamo che l'EQUAZIONE della RETTA PASSANTE per l'ORIGINE DEGLI ASSI è:
y = m · x.
Ora vogliamo trovare il valore di m.
Quando la retta passa per il punto N essa assume i seguenti valori:
b = m · a
b/a = ma/a
b/a = m.
Quindi, l'equazione del primo asintoto è:
y = (b/a) · x.
Per quanto riguarda il secondo asintoto avremo:
y = m · x
-b = m · a
-b/a = ma/a
-b/a = m.
Quindi, l'equazione del secondo asintoto è:
y = (-b/a) · x.






