L'IPERBOLE
Si chiama IPERBOLE il luogo dei punti del piano tali che la DIFFERENZA delle loro DISTANZE da DUE PUNTI FISSI detti FUOCHI è COSTANTE.
Cerchiamo di comprendere meglio questo concetto.
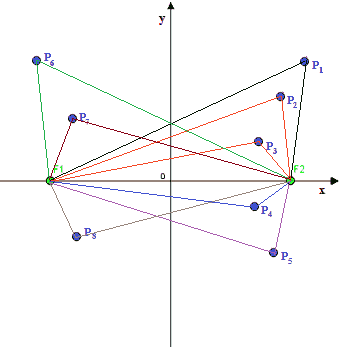
Disegniamo gli assi cartesiani e fissiamo due punti fissi, che saranno i nostri FUOCHI, e che andiamo a chiamare F1 e F2.
Ora disegniamo un punto del piano P1:
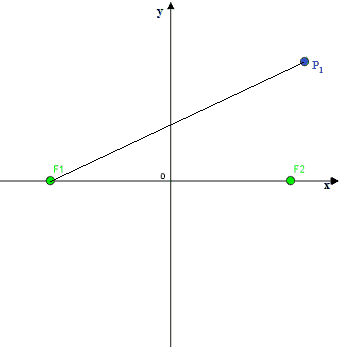
Ora tracciamo la distanza tra il punto P1 e il punto F1:
Quindi tracciamo la distanza tra il punto P1 e il punto F2:
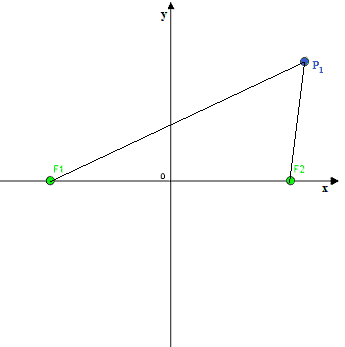
In base alla definizione dell'IPERBOLE abbiamo che:
| P1F1 - P1F2 | = costante.
Indichiamo questa costante con 2a:
| P1F1 -P1F2 | = 2a.
Ora, individuiamo un nuovo punto P2 tale che
| P2F1 -P2F2 | = 2a.
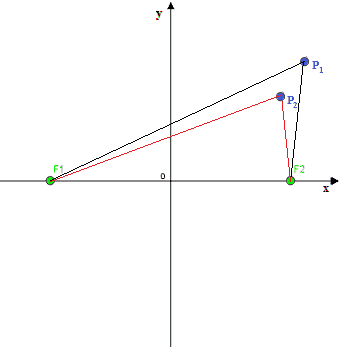
Proseguiamo così disegnando tanti punti P3, P4, ecc..., che soddisfano tutti la condizione data:
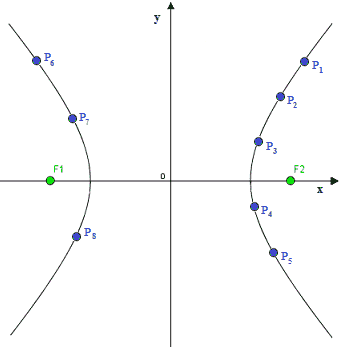
Se colleghiamo tutti i punti tali che la differenza delle loro distante dai fuochi è sempre uguale a 2a abbiamo disegnato una IPERBOLE:
Vedremo, nella prossima lezione, qual è l'equazione dell'iperbole.






