LE FORMULE DEL TEOREMA DI PITAGORA
- Teorema di Pitagora: dimostrazione
- Teorema di Pitagora: dimostrazione
- Triangolo rettangolo
- Quadrato
- Figure geometriche equivalenti e figure geometriche congruenti
- Area del quadrato
- Radice quadrata
Nelle lezioni precedenti abbiamo dimostrato che in un triangolo rettangolo, il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui due cateti.
Possiamo, allora enunciare il TEOREMA DI PITAGORA. Esso afferma che in ogni TRIANGOLO RETTANGOLO l'AREA DEL QUADRATO costruito sull'IPOTENUSA è UGUALE alla SOMMA delle AREE dei QUADRATI costruiti sui due CATETI.
Quindi, dato un triangolo rettangolo
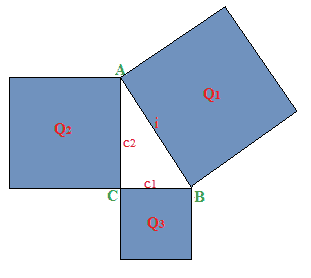
Se chiamiamo rispettivamente con:
- AQ1 l'area del quadrato costruito sull'ipotenusa;
- AQ3 l'area del quadrato costruito sul cateto c1;
- AQ2 l'area del quadrato costruito sul cateto c2;
possiamo scrivere che
AQ1 = AQ2 + AQ3.
Inoltre, abbiamo chiamato con:
- i l'IPOTENUTA del triangolo;
- c1 un CATETO;
- c2 l'altro CATETO.
Noi sappiamo che l'AREA DI un QUADRATO è data da
A = l2
dove
l = lato del quadrato.
Ora, il QUADRATO COSTRUITO SULL'IPOTENUSA, che abbiamo chiamato Q1, ha come lato l'ipotenusa, quindi la sua area sarà data da:
AQ1 = i2.
Il QUADRATO COSTRUITO SUL CATETO 1, che abbiamo chiamato Q3, ha come lato il cateto c1, quindi la sua area
AQ3 = c12.
Infine il QUADRATO COSTRUITO SUL CATETOc2, che abbiamo chiamato Q2, ha come lato il cateto c2, quindi la sua area sarà data da:
AQ2 = c22.
Ora, sostituendo a
AQ1 = AQ2 + AQ3
le rispettive aree possiamo scrivere:
i2 = c12 + c22.
E' chiaro allora che, se noi conosciamo la misura dei due cateti di un triangolo rettangolo e vogliamo sapere la misura dell'ipotenusa dovremo estrarre la radice quadrata della somma dei quadrati dei due cateti. Ovvero:
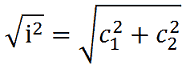
Da cui otteniamo:
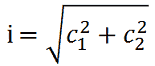
Possiamo allora affermare che la misura dell'IPOTENUSA di un triangolo rettangolo si ottiene estraendo la RADICE QUADRATA della SOMMA dei QUADRATI delle misure dei DUE CATETI.
Nella prossima lezione vedremo alcuni esempi su come applicare tale formula, mentre nelle successive lezioni ci occuperemo delle formule inverse.






