SECONDO TEOREMA DI EUCLIDE
- Poligoni simili
- Similitudine
- Primo teorema di Euclide
- Triangoli simili
- Primo criterio di similitudine dei triangoli
- Secondo criterio di similitudine dei triangoli
- Terzo criterio di similitudine dei triangoli
- Triangoli
- Triangolo rettangolo
- Angolo retto - angolo acuto - angolo ottuso
- Angoli complementari, angoli supplementari, angoli esplementari
- Primo criterio di similitudine dei triangoli
- Proporzioni
- Proporzioni continue
- Proprietà fondamentale delle proporzioni
Dopo aver visto, nella lezione precedente, il PRIMO TEOREMA DI EUCLIDE, ora ci occuperemo del SECONDO TEOREMA DI EUCLIDE.
Disegniamo un TRIANGOLO RETTANGOLO:
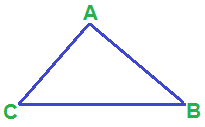
Ora tracciamo l'ALTEZZA RELATIVA ALL'IPOTENUSA:
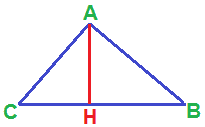
L'altezza AH divide il triangolo ABC in due triangoli: AHC e AHB. Ora osserviamo tali triangoli:
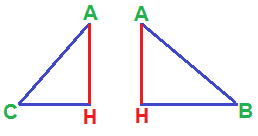
Notiamo che essi:
- hanno ciascuno un ANGOLO
RETTO: si tratta, in entrambi i casi dell'angolo H;
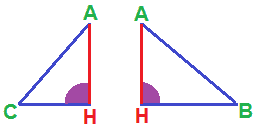
- hanno gli angoli
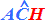 e
e 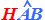 COMPLEMENTARI
dello stesso angolo
COMPLEMENTARI
dello stesso angolo  e
quindi congruenti:
e
quindi congruenti:
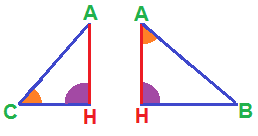
Possiamo allora affermare che i due triangoli hanno DUE ANGOLI CONGRUENTI.
Noi sappiamo che, se in un triangolo due angoli sono congruenti, lo è anche il terzo dato che la somma degli angoli interni di un triangolo è sempre pari a 180°. Ora ricordiamo che il primo criterio di similitudine dei triangoli afferma che se due triangoli hanno i tre ANGOLI ORDINATAMENTE CONGRUENTI sono simili.
Quindi possiamo affermare che i TRIANGOLI AHC e AHB sono SIMILI. Di conseguenza i rapporti tra le coppie di lati corrispondenti sono costanti.
In altre parole, se noi disegniamo nel modo seguente i due triangoli
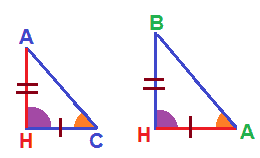
possiamo facilmente scrivere la proporzione
CH : HA = HA : HB
Quella che abbiamo appena scritto è una PROPORZIONE CONTINUA, cioè una proporzione nella quale i due medi (HA) sono uguali e sono detti MEDI PROPORZIONALI.
Osserviamo che:
- il MEDIO PROPORZIONALE è l'ALTEZZArelativa all'ipotenusa (AH) del triangolo rettangolo ABC;
- li estremi della proporzione sono le PROIEZIONI dei due cateti sull'ipotenusa.
In altre parole possiamo dire che in un TRIANGOLO RETTANGOLO, l'ALTEZZA relativa all'ipotenusa è MEDIA PROPORZIONALE fra le PROIEZIONI dei due cateti sull'ipotenusa.
Ora indichiamo con
h la misura dell'altezza relativa all'ipotenusa
pb e pc la misura delle proiezioni dei due cateti sull'ipotenusa
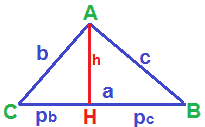
possiamo scrivere la nostra proporzione nel modo seguente:
CH : HA = HA : HB
pb : h = h : pc
Ricordiamo che in una proporzione il prodotto dei medi è uguale al prodotto degli estremi. Quindi possiamo scrivere:
h2 = pb x pc.
Notiamo ora che:
h2 rappresenta l'area del quadrato costruito sull'altezza relativa all'ipotenusa
pb x pc rappresenta l'area del rettangolo che ha per lati le proiezioni dei due cateti sull'ipotenusa
ovvero:
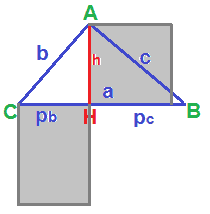
Quindi, il SECONDO TEOREMA DI EUCLIDE afferma che il QUADRATO costruito sull'ALTEZZA RELATIVA ALL'IPOTENUSA è EQUIVALENTE al RETTANGOLO che ha per dimensioni le PROIEZIONI DEI DUE CATETI SULL'IPOTENUSA.






