POLIGONI SIMILI
Disegniamo due triangoli equilateri aventi i lati di diversa lunghezza:
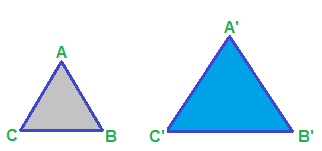
Le due figure da noi disegnate hanno la stessa forma, ma ovviamente la prima figura è più piccola rispetto alla seconda.
Ora disegniamo due quadrati aventi, anche in questo caso, i lati di misura diversa:
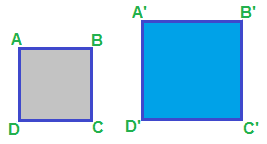
Anche in questo caso le due figure da noi disegnate hanno la stessa forma, ma la prima figura è più piccola rispetto alla seconda.
Due FIGURE che hanno la STESSA FORMA si dicono SIMILI.
Nelle immagini precedenti abbiamo preso in considerazione il caso di un triangolo e quello di un quadrato, ma quanto abbiamo affermato vale per ogni poligono.
Per cui, due POLIGONI che hanno la STESSA FORMA si dicono SIMILI.
Nelle prossime lezioni cercheremo di stabilire quali sono le proprietà che contraddistinguono due poligoni simili.






