PRIMO TEOREMA DI EUCLIDE
- Poligoni simili
- Similitudine
- Triangoli simili
- Primo criterio di similitudine dei triangoli
- Secondo criterio di similitudine dei triangoli
- Terzo criterio di similitudine dei triangoli
- Secondo teorema di Euclide
- Triangoli
- Triangolo rettangolo
- Angolo retto - angolo acuto - angolo ottuso
- Primo criterio di similitudine dei triangoli
- Proporzioni
- Proporzioni continue
- Proprietà fondamentale delle proporzioni
I CRITERI DI SIMILITUDINE dei TRIANGOLI che abbiamo visto nelle lezioni precedenti hanno un'importante applicazione nei due TEOREMI di EUCLIDE.
Tali teoremi trovano applicazione esclusivamente nei TRIANGOLI RETTANGOLI.
In questa lezione ci occuperemo del PRIMO TEOREMA di EUCLIDE, mentre del secondo teorema di Euclide parleremo nella prossima lezione.
Disegniamo un TRIANGOLO RETTANGOLO:
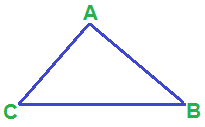
Ora tracciamo l'ALTEZZA RELATIVA ALL'IPOTENUSA:
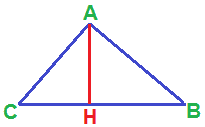
L'altezza AH divide il triangolo in due triangoli: AHC e AHB.
Ora osserviamo i triangoli ABC e AHC
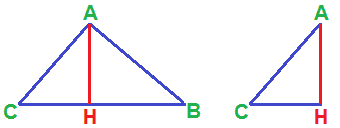
Notiamo che essi:
- hanno ciascuno un ANGOLO RETTO. Nel primo caso si tratta dell'angolo A e nel secondo caso dell'angolo H;
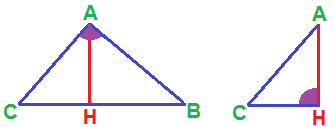
- hanno un ANGOLO IN COMUNE: l'angolo C.
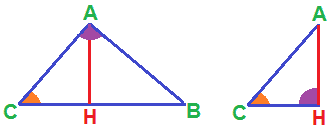
Possiamo allora affermare che i due triangoli hanno DUE ANGOLI CONGRUENTI (l'angolo retto e l'angolo in comune).
Noi sappiamo che, se in un triangolo due angoli sono congruenti , lo è anche il terzo dato che la somma degli angoli interni di un triangolo è sempre pari a 180°. Ora ricordiamo che il primo criterio di similitudine dei triangoli afferma che se due triangoli hanno i tre ANGOLI ORDINATAMENTE CONGRUENTI sono simili.
Quindi possiamo affermare che i TRIANGOLI ABCe AHC sono SIMILI. Di conseguenza i rapporti tra le coppie di lati corrispondenti sono costanti.
In altre parole, se noi disegniamo nel modo seguente i due triangoli
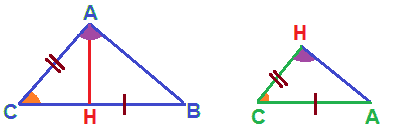
notiamo facilmente che possiamo scrivere la proporzione
CB : CA = CA : CH
Quella che abbiamo appena scritto è una PROPORZIONE CONTINUA, cioè una proporzione nella quale i due medi (CA) sono uguali e sono detti MEDI PROPORZIONALI.
Osserviamo che:
- il MEDIO PROPORZIONALE è un CATETO (CA) del triangolo rettangolo ABC;
- gli estremi
della proporzione sono:
- uno l'IPOTENUSA (CB) del triangolo rettangolo ABC;
- l'altro la PROIEZIONE CH del cateto CA sull'ipotenusa.
In altre parole possiamo dire che in un TRIANGOLO RETTANGOLO, un CATETO è MEDIO PROPORZIONALE fra l'IPOTENUSA e la SUA PROIEZIONE SULL'IPOTENUSA.
Ora indichiamo con
a la misura dell'ipotenusa
b, c le misure dei due cateti
h la misura dell'altezza relativa all'ipotenusa
pb la misura della proiezione CH
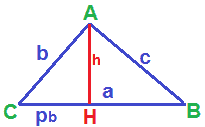
possiamo scrivere la nostra proporzione nel modo seguente:
CB : CA = CA : CH
a : b = b : pb
Ricordiamo che in una proporzione il prodotto dei medi è uguale al prodotto degli estremi. Quindi possiamo scrivere:
b2 = a x pb.
Notiamo ora che:
b2 rappresenta l'area del quadrato costruito sul cateto AC
a x pb rappresenta l'area del rettangolo che ha per lati l'ipotenusa e la proiezione CH di quel cateto sull'ipotenusa
ovvero:
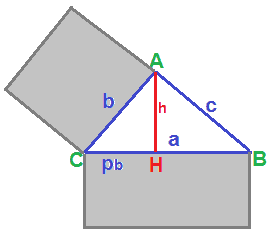
Quindi, il PRIMO TEOREMA DI EUCLIDE afferma che il QUADRATO costruito su un CATETO di un triangolo rettangolo è EQUIVALENTE al RETTANGOLO che ha per dimensioni l'IPOTENUSA e la PROIEZIONE di quel CATETO sull'IPOTENUSA.






