COSTRUZIONE DEL MEDIO PROPORZIONALE TRA DUE SEGMENTI
- Secondo teorema di Euclide
- Il segmento
- Proporzioni
- Proporzioni continue
- Proprietà fondamentale delle proporzioni
- La circonferenza e il cerchio
- Corde di una circonferenza
- Il punto
- Rette perpendicolari
- Triangoli
- Triangolo rettangolo
- Angoli al centro particolari
- Angolo piatto, angolo giro e angolo nullo
- Proprietà degli angoli alla circonferenza
- Angolo retto - angolo acuto - angolo ottuso
Supponiamo di voler COSTRUIRE il SEGMENTO x, MEDIO PROPORZIONALE fra due segmenti dati che misurano rispettivamente p e q.
In altre parole noi vogliamo cercare il segmento x tale che valga la seguente proporzione:
p : x = x : q.
Chiamiamo con CB il segmento pari alla somma di p e q, in altre parole:
CB = p + q.
Ora costruiamo una SEMICIRCONFERENZA il cui DIAMETRO sia il segmento CB:
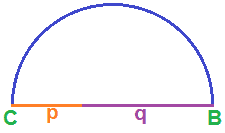
Sul segmento CB segniamo il punto H che rappresenta l'estremo comune al segmento p e al segmento q:
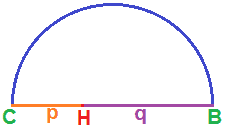
Ora conduciamo la PERPENDICOLARE a CB passante per il punto H fino ad intersecare la semicirconferenza. Chiameremo, il punto di intersezione tra tale perpendicolare e la semicirconferenza, A:
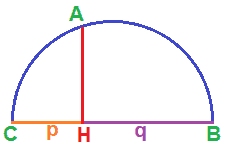
Uniamo i punti A, B e C in modo da ottenere un TRIANGOLO:
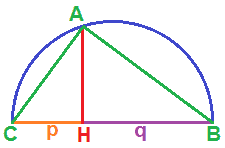
Il triangolo ABC è INSCRITTO nella semicirconferenza: questo triangolo è un triangolo rettangolo. Infatti l'angolo al centro nel nostro caso misura 180° poiché si tratta di un angolo piatto.
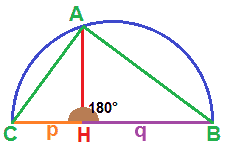
Noi sappiamo che OGNI ANGOLO alla CIRCONFERENZA è la META' dell'ANGOLO al CENTRO che insiste sullo stesso arco. Quindi l'angolo A misura 90° e quindi si tratta di un angolo retto.
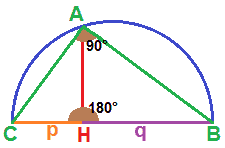
Di conseguenza, il triangolo ABC è un TRIANGOLO RETTANGOLO.
Il segmento che noi stiamo cercando, cioè il segmento x, non è altro che l'altezza relativa all'ipotenusa AH.
Infatti, per il SECONDO TEOREMA di EUCLIDE noi possiamo scrivere:
CH : HA = HA : HB
che equivale a scrivere
p : x = x q.






