PROPRIETA' DEL DETERMINANTE DI UNA MATRICE QUADRATA
- Matrice
- Matrice quadrata
- Determinante di una matrice quadrata
- Calcolo del determinante di una matrice di ordine 3
- Prodotto righe per colonne
- Proprietà del determinante di una matrice quadrata
- Proprietà del determinante di una matrice quadrata
- Proprietà del determinante di una matrice quadrata
- Proprietà del determinante di una matrice quadrata
- Proprietà del determinante di una matrice quadrata
- Proprietà del determinante di una matrice quadrata
- Proprietà del determinante di una matrice quadrata
- Proprietà del determinante di una matrice quadrata
- Proprietà del determinante di una matrice quadrata
Continuiamo l'esame delle PROPRIETA' del DETERMINANTE di una matrice quadrata, parlando dell'ultima proprietà.
X PROPRIETA' del determinante di una matrice quadrata.
Date due matrici quadrate
A e B
abbiamo
det (A · B) = det A · det B.
Esempio.
Consideriamo le matrici A e B:
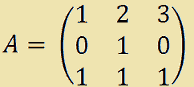
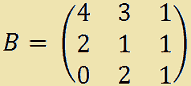
Iniziamo eseguendo il prodotto tra A e B. Avremo:
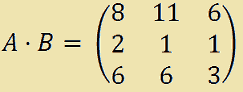
Il determinante del prodotto di A per B è:
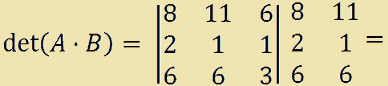
= [(8 · 1 · 3) + (11 · 1 · 6) + (6 · 2 · 6)]+
- [(6 · 1 · 6) + (8 · 1 · 6) + (11 · 2 · 3)] =
= 24 + 66 + 72 - [ 36 + 48 + 66] =
162 - 150 = 12.
Ora calcoliamo il determinante della matrice A e della matrice B separatamente. Avremo:
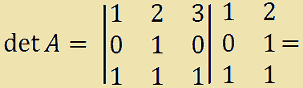
= [(1 · 1 · 1) + (2 · 0 · 1) + (3 · 0 · 1)] +
- [(3 · 1 · 1) + (1 · 0 · 1) + (2 · 0 · 1)] =
= 1 + 0 + 0 - [3 + 0 + 0] =
= 1 - 3 = -2.
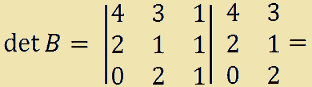
= [(4 · 1 · 1) + (3 · 1 · 0) + (1 · 2 · 2)] +
- [(1 · 1 · 0) + (4 · 1 · 2) + (3 · 2 · 1)] =
= 4 + 0 + 4 - [0 + 8 + 6] =
= 8 - 14 = -6.
Noi abbiamo detto che:
det (A · B) = det A · det B.
Infatti:
12 = (-2)· (-6).
La proprietà che abbiamo appena visto, fa parte di un enunciato che prende il nome di TEOREMA di BINET.
Abbiamo così concluso l'esame delle proprietà dei determinanti di una matrice quadrata.






