PROPRIETA' DEL DETERMINANTE DI UNA MATRICE QUADRATA
- Matrice
- Matrice quadrata
- Determinante di una matrice quadrata
- Calcolo del determinante di una matrice di ordine 3
- Proporzionalità diretta
- Proporzionalità inversa
- Grandezze direttamente proporzionali
- Grandezze inversamente proporzionali
- Proprietà del determinante di una matrice quadrata
- Proprietà del determinante di una matrice quadrata
- Proprietà del determinante di una matrice quadrata
- Proprietà del determinante di una matrice quadrata
- Proprietà del determinante di una matrice quadrata
- Proprietà del determinante di una matrice quadrata
- Proprietà del determinante di una matrice quadrata
- Proprietà del determinante di una matrice quadrata
- Proprietà del determinante di una matrice quadrata
Continuiamo l'esame delle PROPRIETA' del DETERMINANTE di una matrice quadrata.
VII PROPRIETA' del determinante di una matrice quadrata.
Se in una matrice quadrata DUE RIGHE o DUE COLONNE sono PROPORZIONALI il DETERMINANTE è NULLO.
Esempio.
Consideriamo la seguente matrice A:
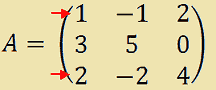
Notiamo che la prima e la terza riga sono tra loro proporzionali: 2 è il rapporto di proporzionalità tra gli elementi della prima riga e i corrispondenti elementi della terza riga.
Calcoliamo il determinante della matrice:
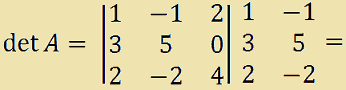
= (1 · 5 · 4) + (-1 · 0 · 2) + [2 · 3 · (-2)] +
- {(2 · 5 · 2) + [1 · 0 · (-2)] + (-1 · 3 · 4)] =
= 20 + 0 - 12 - [20 + 0 - 12] =
= 8 - 8 = 0.
Come possiamo notare il determinante è zero.
Continueremo nelle prossime lezioni ad esaminare altre proprietà del determinante di una matrice.






