EQUAZIONI GONIOMETRICHE FRATTE
- Equazioni goniometriche
- Equazioni goniometriche elmementari del tipo sen x = a
- Equazioni goniometriche riconducibili ad equazioni algebriche
Si chiamano EQUAZIONI GONIOMETRICHE FRATTE quelle equazioni goniometriche nelle quali troviamo una o più FUNZIONI GONIOMETRICHE a DENOMINATORE di una frazione.
La risoluzione di queste equazioni si differenzia dalle altre semplicemente perché occorre porre come CONDIZIONE DI ESISTENZA che il DENOMINATORE sia DIVERSO DA ZERO.
Vediamo, un semplice esempio.
Esempio 1:
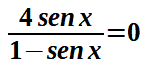
Per prima cosa poniamo come condizione che il denominatore della frazione sia diverso da zero:
1 - sen x ≠ 0
da cui, come abbiamo visto in precedenza, otteniamo:
- sen x ≠ 0
sen x ≠ 0
x ≠ kπ
Questa è la condizione di esistenza della frazione. Ora passiamo a risolverla ricordando che una frazione è uguale a zero quando il suo numeratore è uguale a zero. Quindi possiamo scrivere:
4 sen x = 0
da cui:
sen x = 0
x = kπ
La soluzione è inammissibile, quindi l'equazione non ammette soluzioni.
Un'osservazione da fare è la seguente: se a denominatore della frazione abbiamo la TANGENTE occorre porre due CONDIZIONI DI ESISTENZA:
- la prima è che la TANGENTE sia DIVERSA DA ZERO;
- poiché la tangente non è altro che il RAPPORTO tra il SENO e il COSENO, sarà necessario porre come ulteriore condizione di esistenza che anche il COSENO sia DIVERSO DA ZERO.
Esempio 2:
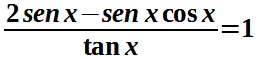
Per prima cosa poniamo come condizione che il denominatore della frazione sia diverso da zero:
tan x ≠ 0
da cui ricaviamo
x ≠ kπ.
Poi, come abbiamo detto, dobbiamo porre come ulteriore condizione che
cos x ≠ 0
che, abbiamo visto in una precedente lezione, equivale a dire:
x ≠ π/2 + kπ.
Ora portiamo 1 a primo membro, cambiandogli di segno, e calcoliamo il mimino comune multiplo:
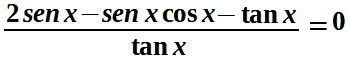
Una frazione è uguale a zero quando il numeratore è uguale a zero, quindi possiamo scrivere:
2 sen x - sen x cos x - tan x = 0
Scriviamo la tangente come il rapporto tra seno e coseno:
2 sen x - sen x cos x - (sen x/ cos x) = 0
Moltiplichiamo primo e secondo membro per cos x:
2 sen x cos x - sen x cos2 x = sen x
Portiamo a primo membro sen x cambiandogli di segno:
2 sen x cos x - sen x cos2 x - sen x = 0
Mettiamo in evidenza sen x
sen x (2 cos x - cos2 x - 1) = 0
Per la legge di annullamento del prodotto l'equazione è uguale a zero quando:
sen x = 0
oppure quando
2 cos x - cos2 x - 1 = 0
o quando entrambe si annullano.
Dalla prima ricaviamo:
Questa soluzione non è ammissibile date le condizioni di esistenza poste.
Passiamo a
2 cos x - cos2 x - 1 = 0
Questa equazione è riconducibile ad un'equazione algebrica e la risolviamo ponendo:
y = cos x
e ricaviamo:
2y - y2 - 1 = 0.
Ordiniamo e risolviamo:
- y2 - 2y - 1 = 0.
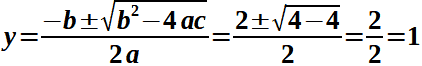
Sostituendo abbiamo:
cos x = 1
Quest'ultima soluzione è ammissibile ed è anche la soluzione dell'equazione goniometrica data.
Facciamo un'ultima osservazione: se a denominatore abbiamo la COTANGENTE, dobiamo porre come condizione sia che la cotangente sia DIVERSA DA ZERO, sia che il SENO sia DIVERSO DA ZERO, essendo la cotangente il rapporto tra seno e coseno.






