EQUAZIONE DELLA RETTA TANGENTE ALLA CIRCONFERENZA E PERPENDICOLARE AD UNA RETTA DATA
- Equazione della circonferenza
- Posizione di una retta rispetto ad una circonferenza
- Equazione della retta tangente alla circonferenza e passante per un punto P
- Equazione della retta tangente alla circonferenza e passante per un punto P appartenente alla circonferenza
- Formule di sdoppiamento nella circonferenza
- Equazione della retta tangente alla circonferenza e passante per un punto P
- Equazione della retta tangente alla circonferenza e passante per un punto P
- Equazione della retta tangente alla circonferenza e parallela ad una retta data
- Retta perpendicolare ad una retta data e passante per un punto
- Coefficiente angolare
A volte capita di dover scrivere l'equazione della RETTA TANGENTE ad una CIRCONFERENZA conoscendo:
- l'equazione della CIRCONFERENZA;
- l'equazione di una RETTA PERPENDICOLARE alla tangente cercata. Questa retta la chiamiamo y' e ipotizziamo che abbia come equazione
y' = m'x + n'.
Il problema si risolve in maniera simile a quanto visto nella lezione precedente.
Ovviamente dobbiamo ricordare che due RETTE sono PERPENDICOLARI quando il COEFFICIENTE ANGOLARE dell'una e il RECIPROCO del coefficiente angolare dell'altra preso con segno OPPOSTO.
Quindi, data l'equazione generale della retta:
y = mx + n
e poiché deve essere
m = -1/m'
possiamo scrivere
y = (-1/m')· x + n.
A questo punto si procede come sempre:
- mettiamo a SISTEMA
l'equazione della CIRCONFERENZA
con l'equazione della RETTA
appena trovata;
- SOSTITUIAMO,
nell'equazione della circonferenza, alla
y il valore
(-1/m') · x + n
- poniamo la CONDIZIONE
di TANGENZA,
Δ = 0.
- andiamo a cercare il valore del TERMINE
NOTO n;
- SOSTITUIAMO il valore del termine noto nell'equazione della retta y. Abbiamo così trovato l'equazione della retta tangente alla circonferenza e perpendicolare alla retta data.
Esempio:
scrivere l'equazione della retta perpendicolare alla retta y = 1/2x - 9 e tangente alla circonferenza di equazione x2 + y2 + 4x + 2y - 15 = 0
La retta da noi cercata è del tipo:
y = mx + n.
Questa retta deve essere perpendicolare alla retta
y = 1/2x - 9
cioè il coefficiente angolare della retta tangente alla circonferenza deve essere
-2.
Quindi la retta che cerchiamo ha come equazione
y = -2x + n.
Ora scriviamo il sistema formato dalla equazione della circonferenza e dall'equazione di questa retta:
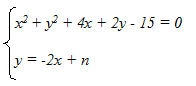
Nell'equazione della circonferenza, sostituiamo la y con -2x + n:
x2 + y2 + 4x + 2y - 15 = 0
x2 + (-2x + n)2 + 4x + 2(-2x + n) - 15 = 0
x2 + 4x2 + n2 - 4nx + 4x - 4x + 2n - 15 = 0
5x2
- 4nx + n2 + 2n - 15 = 0.
Poniamo la condizione di tangenza
Δ = 0
b2 - 4ac = 0
16n2 - 4 · (5) · (n2 + 2n - 15) = 0
16n2 - 20n2 + 40n + 300 = 0
- 4n2 + 40n + 300 = 0
4n2
- 40n - 300 = 0.
Cerchiamo il valore di n:
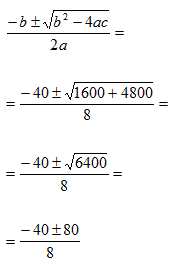
Quindi le due soluzioni sono:
n1 = (-40 - 80)/ (8) = -120/(8) = -1
n2 = (-40 + 80)/ (8) = 40/8 = 5.
Quindi le due rette tangenti alla circonferenza e perpendicolari alla retta data sono:
y = -2x + 5
y = -2x - 15.






