EQUAZIONE DELLA RETTA TANGENTE ALLA CIRCONFERENZA E PASSANTE PER UN PUNTO P APPARTENENTE ALLA CIRCONFERENZA
- Equazione della circonferenza
- Equazione della circonferenza dati il centro e il raggio
- Posizione di una retta rispetto ad una circonferenza
- Equazione della retta tangente alla circonferenza e passante per un punto P
- Fascio di rette passanti per un punto
- Equazione della retta passante per due punti
- Coefficiente angolare
- Retta perpendicolare ad una retta data e passante per un punto
Dopo la breve introduzione fatta, nella lezione precedente, iniziamo a vedere come possiamo scrivere l'EQUAZIONE della RETTA TANGENTE alla circonferenza. Partiamo dal caso in cui conosciamo
- l'EQUAZIONE
DELLA CIRCONFERENZA;
- le COORDINATE
di un punto P(x0;
y0) che
sappiamo APPARTENERE alla
circonferenza.
Disegniamo il caso in cui il punto P(x0; y0) APPARTIENE alla circonferenza.
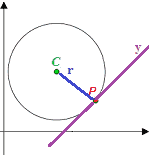
Notiamo che, il raggio r e la retta y sono tra loro PERPENDICOLARI. Per cui, se troviamo l'equazione della retta a cui appartiene il segmento C, cioè il raggio, tale retta è perpendicolare alla retta y. E sappiamo che due rette sono perpendicolari quando
m' = - 1/m.
Ora, per risolvere il nostro problema procediamo nel modo seguente:
- scriviamo il FASCIO
di RETTE passante per P.
Ricordiamo che la formula è
y - y0 = m (x - x0)
- determiniamo
le COORDINATE del CENTRO
C (α; β)
della circonferenza sapendo che
-2α = a
-2β = b
- scriviamo l'EQUAZIONE
della RETTA passante per P
e per C.
Ricordiamo che essa è:
(y - y0)/ (y1 - y0)= (x - x0)/ (x1 - x0)
-
calcoliamo il COEFFICIENTE
ANGOLARE della retta passante per
P e
per C;
- troviamo il COEFFICIENTE ANGOLARE
della retta y e lo
sostituiamo nel FASCIO DI RETTE passante
per P in
modo da trovare l'equazione della
retta tangente alla circonferenza.
Esempio:
scrivere l'equazione della retta tangente, nel punto P(8; 6), alla circonferenza di equazione x2 + y2 -10x + 6y -56 = 0.
Il problema ci dice qual è il punto in cui cui la retta è tangente alla circonferenza: dunque questo punto appartiene sia alla retta che alla circonferenza.
Iniziamo scrivendo il fascio di rette passante per il punto P:
y - y0 = m (x - x0)
y - 6 = m(x - 8).
Ora troviamo le coordinate del centro della circonferenza:
-2α = - 10
-2β = 6
da cui ricaviamo
-2α = - 10
2α = 10
α = 5
e
-2β = 6
2β = - 6
β = -3.
Quindi C ha coordinate
C(5; -3).
Ora scriviamo l'equazione della retta passante per i punti C e P:
(y - y0)/ (y1 - y0)= (x - x0)/ (x1 - x0)
(y - 6)/ (-3 - 6)= (x - 8)/ (5 - 8)
(y - 6)/ -9 = (x - 8)/ (-3)
y - 6 = 3x - 24
y = 3x - 24 + 6
y = 3x -18.
Il coefficiente angolare della retta passante per i punti C e P è 3.
Poiché tale retta è perpendicolare alla retta y, il coefficiente angolare della retta y sarà -1/3.
Sostituiamo tale valore nella equazione del fascio di rette passante per P e avremo:
y - 6 = m(x - 8).
y - 6 = -1/3(x - 8)
y - 6 = -1/3x + 8/3
y = -1/3x + 8/3 + 6
y = -1/3x + (8+18)/3
y = -1/3x + 26/3.
Abbiamo trovato l'equazione della retta tangente alla circonferenza data nel punto P (appartenente alla circonferenza).
Nella prossima lezione vedremo come, questo tipo di problema, può essere risolto anche applicando le formule di sdoppiamento.






