EQUAZIONE DELLA CIRCONFERENZA
- Equazione della circonferenza: alcune considerazioni
- Equazione della circonferenza dati il centro e il raggio
- La circonferenza e il cerchio
- Il punto
- Distanza tra due punti sul piano
- Distanza tra due punti sul piano cartesiano
- Radice quadrata
- Radice quadrata di una potenza
- Quadrato di un binomio
La CIRCONFERENZA è il luogo geometrico dei PUNTI EQUIDISTANTI da un PUNTO FISSO detto CENTRO.
Disegniamo una circonferenza di centro
C (α; β)
che si legge
"C di coordinate Alfa e Beta".
e raggio r:
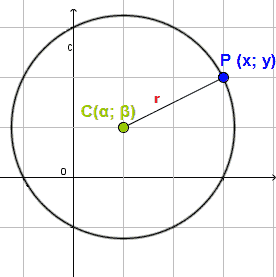
Indichiamo con c (minuscolo) la nostra circonferenza.
Un generico punto P di coordinate x ed y, appartiene alla circonferenza se, e solamente se, la sua distanza dal centro C è pari ad r.
Ora, ricordando che, dati due punti
P1 (x1; y1)
P2 (x2; y2)
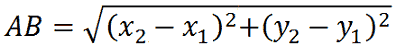
Quindi, la distanza tra il punto P(x; y) e il punto C (α; β) è

Affinché il punto P appartenga alla circonferenza c è necessario che tale distanza sia uguale al raggio r, ovvero:

Quindi P appartiene alla circonferenza c solo, e solo se, è vero che:

Eleviamo, primo e secondo membro al quadrato, in modo da togliere la radice quadrata a primo membro:

da cui otteniamo

Ora sviluppiamo, applicando la formula del quadrato di un binomio:

Ora portiamo a primo membro r2 cambiando di segno:

A questo punto poniamo:
-2α = a
-2β = b
α2 + β2 - r2 = c .
Quindi, la nostra equazione diventa
x2 + α2 - 2xα + y2 + β2 - 2yβ - r2 = 0
x2 + y2 + ax + by + c = 0.
Quindi, l'equazione di una circonferenza è:
x2 + y2 + ax + by + c = 0.
Questa equazione è detta in FORMA NORMALE o CANONICA.
Vedremo, nelle prossime lezioni, che in alcuni casi può essere più utile usare l'equazione

che abbiamo visto poco sopra.






