ELEMENTI E PUNTI NOTEVOLI DEL TRIANGOLO EQUILATERO
- Triangoli
- Elementi del triangolo
- Triangolo equilatero
- Elementi e punti notevoli di un triangolo
- Altezze di un triangolo
- Ortocentro
- Mediane
- Baricentro
- Bisettrici
- Incentro
- Assi dei lati di un triangolo
- Circocentro
- Figure geometriche equivalenti e figure geometriche congruenti
In questa lezione andremo a vedere le caratteristiche che ALTEZZE, MEDIANE, BISETTRICI e ASSI assumono in un TRIANGOLO EQUILATERO.
Disegniamo il TRIANGOLO EQUILATERO ricordando che esso è un triangolo i cui LATI e i cui ANGOLI sono CONGRUENTI:
Noi sappiamo che un TRIANGOLO EQUILATERO è anche un TRIANGOLO ISOSCELE, quindi valgono anche per il triangolo equilatero le considerazioni fatte, nelle lezione precedente, per il triangolo isoscele.
Quindi possiamo affermare che in un TRIANGOLO EQUILATERO ALTEZZA, MEDIANA, BISETTRICE e ASSE di ogni lato COINCIDONO in un unico segmento.
Proviamo a disegnarli, avremo:
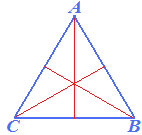
Osserviamo che nel TRIANGOLO ISOSCELE l'ASSE del TRIANGOLO relativo alla BASE COINCIDE con l'ALTEZZA, con la MEDIANA e con la BISETTRICE.
Nel TRIANGOLO EQUILATERO, essendo tutti e tre i lati uguali, l'ASSE di ogni lato COINCIDE con l'ALTEZZA, con la MEDIANA e con la BISETTRICE.
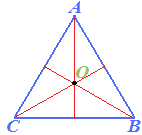
Vediamo ora l'ORTOCENTRO, il BARICENTRO, l'INCENTRO, e il CIRCOCENTRO: essi non solo appartenengono al segmento che rappresenta al tempo stesso l'altezza, la bisettrice, la mediana e gli assi del triangolo, ma COINCIDONO in un UNICO PUNTO che prende il nome di CENTRO del TRIANGOLO EQUILATERO e che nella figura sottostante abbiamo indicato con la lettera O: