INCENTRO
- Triangoli
- Elementi del triangolo
- Triangolo rettangolo
- Elementi e punti notevoli di un triangolo
- Bisettrici
- Distanza di un punto da una retta
- Figure geometriche equivalenti e figure geometriche congruenti
Nella lezione precedente abbiamo parlato delle BISETTRICI di un triangolo e dell'INCENTRO e abbiamo appreso che si chiama BISETTRICE di un triangolo RELATIVA AD UN VERTICE il SEGMENTO che UNISCE il VERTICE al LATO OPPOSTO DIVIDENDO a META' l'angolo.
LE TRE BISETTRICI di un triangolo si INCONTRANO in un punto detto INCENTRO che nel nostro disegno abbiamo evidenziato con la lettera O:
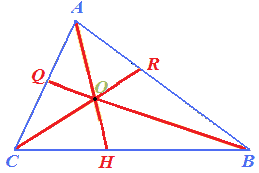
Sappiamo, inoltre, che qualsiasi triangolo noi disegniamo l'INCENTRO è sempre INTERNO al triangolo.
Ora consideriamo la DISTANZA dell'INCENTRO da ciascuno dei tre lati AB, BC, AC.
Ricordiamo che la DISTANZA di un PUNTO da una RETTA è la LUNGHEZZA DEL SEGMENTO DI PERPENDICOLARE condotta da quel punto alla retta.
Allora disegniamo la distanza dell'incentro da ciascuno dei tre lati. Evidenziamo i relativi segmenti con il colore verde:
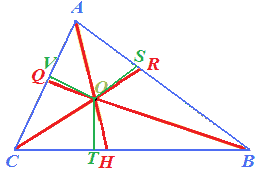
I segmenti OS, OT e OV rappresentano le DISTANZE dell'INCENTRO dai lati AB, BC e AC.
Notiamo, inoltre, che i segmenti OS, OT e OV sono CONGRUENTI hanno cioè tutti la stessa lunghezza.
Possiamo allora affermare che, in un qualsiasi triangolo, l'INCENTRO è EQUIDISTANTE dai TRE LATI.






