FUNZIONE OMOGRAFICA
- L'iperbole
- Equazione dell'iperbole
- Asintoti dell'iperbole
- Iperbole traslata
- Iperbole equilatera riferita agli assi
- Iperbole equilatera riferita ai suoi asintoti
- Campo di esistenza di una frazione algebrica
- Assi cartesiani ortogonali
- Traslazione degli assi cartesiani
- Equazione della retta
- Retta parallela all'asse delle x
- Rette parallele
- Funzioni reali di variabile reale
Con l'espressione FUNZIONE OMOGRAFICA si intende una funzione del tipo
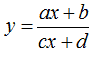
Questa funzione può rappresentare tre luoghi geometrici diversi:
- Quando
c = 0
la funzione rappresenta una RETTA di equazione
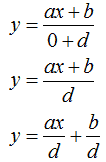
d ≠ 0
- Quando
c ≠ 0 e ad = bc
la funzione rappresenta una RETTA ORIZZONTALE. Infatti, se
ad = bc
avremo
ad/c = bc/c
ad/c = b.
Quindi partiamo da
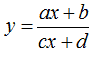
e poniamo
b = ad/c .
Avremo:
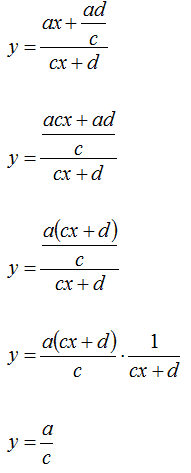
Attenzione però! Abbiamo detto che questa è una retta orizzontale, ma tranne in un punto cioè:
x = -d/c.
Infatti, il campo di esistenza di questa frazione è appunto
c ≠ 0 - che sicuramente è vera perché posta nelle condizioni di partenza
e
cx + d ≠ 0
da cui segue
cx ≠ -d
x ≠ -d/c.
- Quando
c ≠ 0 e ad ≠ bc
la funzione rappresenta un'IPERBOLE EQUILATERA riferita ai suoi ASINTOTI e TRASLATA rispetto agli ASSI CARTESIANI:
In altre parole ci troviamo di fronte ad un'iperbole del tipo:
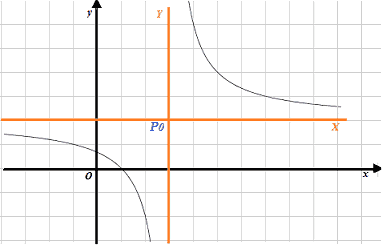
Questa iperbole è detta anche IPERBOLE OMOGRAFICA.
Dimostriamo che, l'equazione vista sopra, rappresenta un'iperbole equilatera riferita ai suoi asintoti e traslata rispetto agli assi cartesiani. Ricordiamo che l'equazione di un'iperbole equilatera riferita ai suoi asintoti è del tipo:
xy = k
da cui si ottiene
y = k/ x.
Come di consueto indichiamo con X e Y gli assi aventi per origine il punto P0: essi rappresentano gli ASINTOTI della nostra iperbole.
Supponiamo che il punto P0 abbia come coordinate
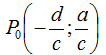
Ovviamente dovrà essere
c ≠ 0 - che sicuramente è vera perché posta nelle condizioni di partenza.
Vediamo l'equazione che l'iperbole assume se il sistema di riferimento è dato dagli assi XP0 Y. Essa sarà del tipo:
XY = k.
Noi, però, vogliamo sapere qual è l'equazione di tale iperbole sul sistema di assi xOy.
Avvaliamoci delle equazioni che ci permettono di passare alle coordinate del sistema xOy. Queste equazioni sono:
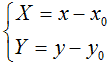
dove x0 e y0 sono le coordinate del punto P0 che nel nostro caso sono
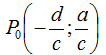
Effettuiamo le dovute sostituzioni e avremo:
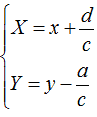
da cui avremo
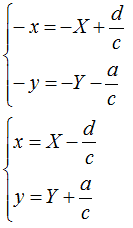
Sostituiamo nell'equazione
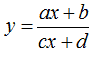
i valori di x e y appena trovati e ricordiamo, che
k =a2/2.
Quindi abbiamo:
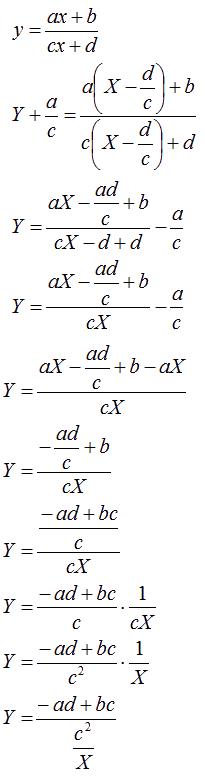
Come possiamo notare la nostra equazione assume la forma:
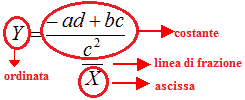
La nostra equazione, quindi, è quella di un'iperbole equilatera riferita ai propri asintoti e traslata.
Nella prossima lezione vedremo gli elementi di tale iperbole.






