ELEMENTI DELL'IPERBOLE EQUILATERA RIFERITA AI SUOI ASINTOTI
- L'iperbole
- Equazione dell'iperbole
- Iperbole equilatera riferita agli assi
- Iperbole equilatera riferita ai suoi asintoti
- Diagonale di un poligono
- Quadrato
- Figure geometriche equivalenti e figure geometriche congruenti
- Teorema di Pitagora e diagonale del quadrato
Nella lezione precedente abbiamo visto che l'EQUAZIONE dell'IPERBOLE EQUILATERA riferita ai suoi ASINTOTI è
xy = ±k
con
k > 0
quando i rami dell'iperbole si trovano nel PRIMO e TERZO quadrante
e con
k < 0
quando i rami dell'iperbole si trovano nel SECONDO e QUARTO quadrante.
L'iperbole di equazione
xy = +k
ha:
- FUOCHI
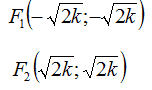
Infatti, nella lezione precedente abbiamo detto che
F1 (a; a)
F2 (-a; -a)
e abbiamo posto
a2/2 = k
da cui abbiamo
a2 = 2k
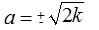
- VERTICI
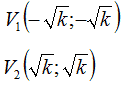
Infatti se osserviamo l'immagine riportata sotto
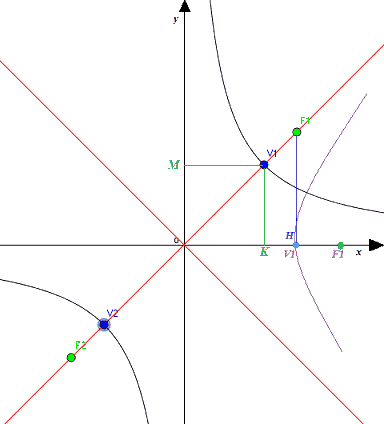
notiamo che il segmento OV1 è pari ad a, ma esso è anche la diagonale del quadrato OKV1M dato che i segmenti OK e MV1 sono congruenti. Allora poniamo
OK = MV1 = l
Applicando il teorema di Pitagora possiamo scrivere:
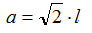
da cui otteniamo
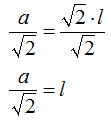
Quindi il segmento OK non è altro che il rapporto tra a e la radice di 2. La stessa cosa si può dire per il segmento MV1.
Ma poiché noi abbiamo posto
a2/2 = k
da cui abbiamo
a2 = 2 k
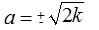
possiamo scrivere che
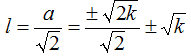
-
ASINTOTI
x = 0
y = 0
dato che essi non sono altro che gli assi cartesiani.
In modo del tutto simile possiamo dire che l'iperbole di equazione
xy = -k
ha:
- FUOCHI
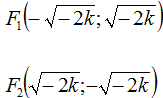
- VERTICI
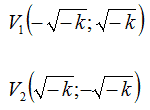
- ASINTOTI
x = 0
y = 0
dato che, anche in questo caso, si tratta degli assi cartesiani.






