FUNZIONI REALI DI VARIABILE REALE
- Corrispondenza univoca
- Corrispondenza biunivoca
- Funzioni matematiche
- L'insieme dei numeri reali
- Definizione di numeri reali
- Nozione di insieme
- Sottoinsiemi di un insieme
Dallo studio della proporzionalità si è appreso che date due GRANDEZZE VARIABILI
x ed y
tali che:
- x appartiene all'insieme X
- ed y appartiene all'insieme Y
ovvero
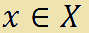
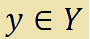
si dice che
y è funzione di x
che si scrive
y = f(x)
se
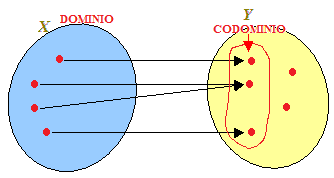
ad OGNI ELEMENTO di X CORRISPONDE UNO E UN SOLO ELEMENTO di y.
y = f(x)
si legge
y uguale effe di x.
Nel nostro esempio:
- x è la variabile INDIPENDENTE
-
y è la variabile DIPENDENTE.
Ora poniamo la condizione che l'INSIEME X e l'INSIEME Y coincidano entrambi con l'INSIEME R dei NUMERI REALI o con dei suoi sottoinsiemi.
In questo caso possiamo parlare di FUNZIONE REALE di VARIABILE REALE per indicare una CORRISPONDENZA che associa ad un NUMERO REALE x appartenente ad X UNO E UN SOLO NUMERO REALE y appartenente ad Y.
ATTENZIONE!! Non è detto il viceversa, cioè non è detto che ad ogni y appartenente all'insieme Y corrisponda uno e un solo elemento di x dell'insieme X.
L'INSIEME X è detto:
- DOMINIO;
- INSIEME DI DEFINIZiONE;
- CAMPO DI ESISTENZA
della funzione.
L'insieme degli elementi y appartenenti ad Y che hanno CORRISPONDENTI in X si chiamano CODOMINIO della funzione.
Il CODOMINIO è l'INSIEME DELLE IMMAGINI degli elementi x appartenenti ad X.
f è la LEGGE DI CORRISPONDENZA cioè il legame che associa la variabile dipendente y alla variabile indipendente x.