EQUAZIONI GONIOMETRICHE ELEMENTARI NELLA SECANTE
Vediamo, ora, come si risolvono le EQUAZIONI GONIOMETRICHE ELEMENTARI NELLA SECANTE, ovvero le equazioni che si presentano nel modo seguente:
sec x = n
con
n ∈ R
che si legge
n appartenente all'insieme dei numeri reali.
Innanzitutto occorre precisare che l'equazione AMMETTE SOLUZIONI SOLAMENTE SE
n ≤ -1
oppure
n ≥ +1.
Fatta questa premessa ricordiamo che la SECANTE è la FUNZIONE INVERSA del COSENO. Di conseguenza, scrivere
sec x = n
equivale a scrivere
1/cos x = n.
Questo significa che affinché la frazione non perda di significato è necessario che il coseno di x sia DIVERSO DA ZERO.
Noi sappiamo che il coseno di un arco è diverso da zero, quando l'arco è diverso da π/2 + kπ, quindi la soluzione da noi trovata dovrà essere
x ≠ π/2 + kπ
con
Fatta questa premessa è evidente che la nostra equazione è riconducibile ad un'EQUAZIONE GONIOMETRICA ELEMENTARE NEL COSENO
Infatti:
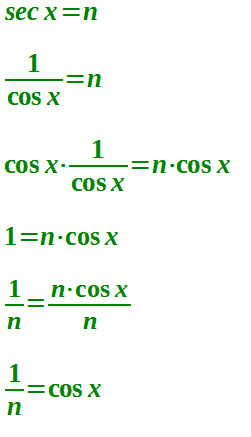
Quindi risolvere l'equazione:
sec x = n
Equivale a risolvere l'equazione:
cos x = 1/n.
Esempio:
sec x = 2
Per prima cosa osserviamo che la nostra equazione ammette soluzioni essendo n ≥ 1.
Quindi, andiamo a cercare le soluzioni:
sec x = 2
cos x = 1/2
x = ± π/3 + 2kπ
con
Essendo la soluzione trovata diversa da π/2 + kπ essa è accettabile.






