EQUAZIONI GONIOMETRICHE ELEMENTARI DEL TIPO
cos x = b
Dopo aver visto come si risolvono le equazioni goniometriche elementari nel seno, ora passiamo ad esaminare le EQUAZIONI GONIOMETRICA ELEMENTARE NEL COSENO, ovvero le equazioni che si presentano nella forma:
cos x = b
con b appartentene all'insieme dei numeri reali, ovvero
con b ∈ R
che si legge
b appartenente all'insieme dei numeri reali.
Prima di passare alla risoluzione dell'equazione, dobbiamo andare ad esaminare il valore di b. Come sappiamo, il coseno assume sempre valori compresi tra -1 e +1 qualuque sia il valore dell'angolo orientato. Di conseguenza, affinché l'equazione possa essere risolta, è necessario che b sia compreso tra -1 e +1, con -1 e +1 compresi. Quindi è necessario che:
-1 ≤ b ≤ +1.
Se invece b assume valori al di fuori di questo intervallo allora sicuramente l'equazione è impossibile.
Esempio:
cos x = -2
non ha significato e l'equazione NON AMMETTE SOLUZIONI.
Così come abbiamo già visto per l'equazione gonimetrica elementare nel seno, anche per quella nel coseno possiamo senz'altro dire che, se la funzione ammette soluzioni, esse sono INFINITE e si RIPETONO PERIODICAMENTE, dato che le funzioni goniometriche sono tutte FUNZIONI PERIODICHE. Nel caso della funzione coseno il PERIODO è pari a 2kπ. Quindi, alle soluzioni che andremo a trovare dovremo sempre aggiungere tutte le soluzioni che si ottengono compiendo k giri completi della circonferenza goniometrica.
A questo punto vediamo come si risolvono le funzioni goniometriche periodiche nel coseno: il modo di procedere è simile a quello visto nel caso delle funzioni goniometriche elementari nel seno.
Disegniamo la CIRCONFERENZA GONIOMETRICA:
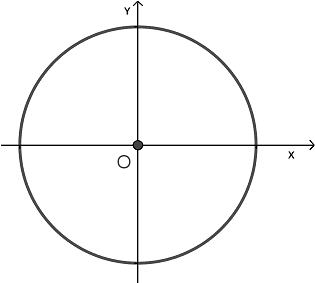
Indichiamo gli assi cartesiani con X ed Y MAIUSCOLI in modo da non confonderli con l'incognita x.
Noi sappiamo che il coseno di un angolo orientato non è altro che l'ASCISSA del punto della circonferenza goniometrica associato all'angolo stesso.
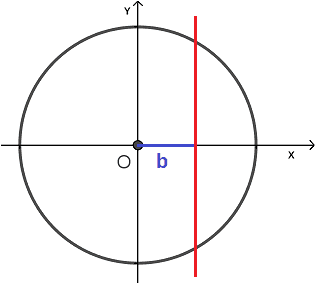
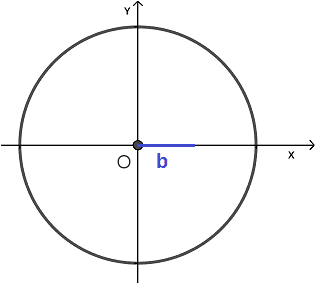
Quindi andiamo a disegnare, sull'asse delle X, un segmento la cui misura è pari a b. Poiché l'asse delle ascisse è orientata verso destra:
- se b è POSITIVO disegneremo il segmento partendo dall'origine degli assi e andando VERSO DESTRA;
- se b è NEGATIVO disegneremo il segmento partendo dall'origine degli assi e andando VERSO SINISTRA.
In questo caso supponiamo che b sia un numero positivo.
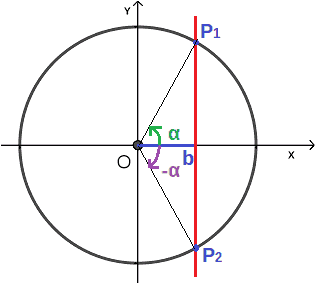
Andiamo a tracciare una RETTA PARALLELA all'ASSE delle Y e passante per l'estremo, diverso dall'origine degli assi, del segmento b:
Pubblicità/Advertising
I due PUNTI, che chiamiamo P1 e P2, nei quali tale retta interseca la circonferenza goniometrica, rappresentano i punti associati rispettivamente agli archi α e 2π - α.
Ma noi sappiamo che
Quindi possiamo dire che i due archi che hanno il conseno pari a b sono α e -α.
Quindi, data l'equazione goniometrica
cos x = b
le soluzioni saranno:
x = + α
oppure
x = - α
o entrambi.
Data la periodicità della funzione coseno, bisogna aggiungere anche tutte quelle soluzioni che si ottengono compiendo k giri completi della circonferenza goniometrica. Di conseguenza, la soluzione della nostra equazione goniometrica sarà:
x = α + 2kπ
oppure
x = - α + 2kπ
che possiamo scrivere anche nel modo seguente:
x = ±α +2kπ
con
Ovviamente, lo stesso risultato, può essere scritto anche in gradi, ovvero:
x = ±α° + k·360°
con
Nella prossima lezione vedremo alcuni esempi su come risolvere praticamente le equazioni goniometriche elementari nel coseno.
