EQUAZIONI GONIOMETRICHE ELEMENTARI NELLA COSECANTE
In questa lezione ci occuperemo della risoluzione delle EQUAZIONI GONIOMETRICHE ELEMENTARI NELLA COSECANTE, ovvero delle equazioni che si presentano nel modo che segue:
cosec x = n
con
n ∈ R
che si legge
n appartenente all'insieme dei numeri reali.
Questa equazione AMMETTE SOLUZIONI SOLAMENTE SE
n ≤ -1
oppure
n ≥ +1.
Per risolvere questo tipo di equazioni occorre ricordare che la COSECANTE è la FUNZIONE INVERSA del SENO. Di conseguenza, l'equazione
cosec x = n
può essere scritta anche nel modo seguente
1/sen x = n.
Quindi, l'equazione goniometrica elementare nella cosencante può essere ricondotta ad un'EQUAZIONE GONIOMETRICA ELEMENTARE NEL SENO. Infatti:
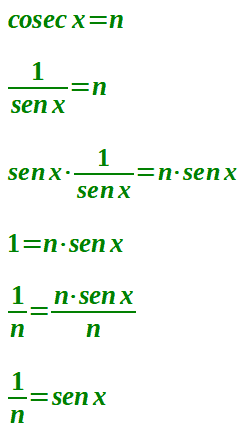
E' evidente, allora, che affinché la frazione non perda di significato è necessario che il seno di x sia DIVERSO DA ZERO.
Noi sappiamo che il seno di un arco è diverso da zero, quando l'arco è diverso da kπ, quindi la soluzione da noi trovata dovrà essere
x ≠ kπ
con
Quindi risolvere l'equazione:
cosec x = n
equivale a risolvere l'equazione:
sen x = 1/n.
Esempio:
cosec x = 2
Per prima cosa osserviamo che la nostra equazione ammette soluzioni essendo n ≥ 1.
Quindi, andiamo a cercare le soluzioni:
cosec x = 2
sen x = 1/2
x = π/6 + 2kπ
oppure
x = (π - π/6) + 2kπ
Da quest'ultima soluzione, eseguendo i calcoli indicati in parentesi, ricaviamo:
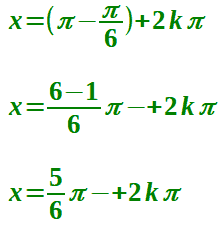
Quindi le due suoluzioni sono:
x = π/6 + 2kπ ∨ x = 5/6π + 2kπ
con
Essendo le due soluzioni diverse da kπ esse sono entrambe accettabili.






