EQUAZIONI CON VALORE ASSOLUTO ED INCOGNITA ANCHE FUORI DAL MODULO
- Nozione di valore assoluto
- Equazioni con valore assoluto
- Equazioni con valore assoluto e lo zero
- Equazioni con valore assoluto ed una costante
- Equazioni con due moduli
- Equazioni con due moduli
- Equazioni con tre o più moduli
- Equazioni con un valore assoluto dentro l'altro
- Equazioni fratte con valore assoluto
- Risoluzione di equazioni con valore assoluto
Passiamo ad esaminare quelle EQUAZIONI CON VALORE ASSOLUTO nelle quali abbiamo:
-
in un membro il MODULO con l'INCOGNITA;
- nell'altro membro l'INCOGNITA FUORI DAL MODULO.
La nostra equazione avrà la forma:
|A(x)| = B(x).
Ora torniamo per un attimo alla DEFINIZIONE DI VALORE ASSOLUTO. Essa è:
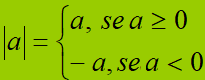
Quindi possiamo dire che quando
A(x) ≥ 0
la nostra equazione sarà
A(x) = B(x).
Il che significa risolvere il sistema:
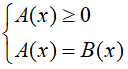
Quando, invece
A(x) < 0
la nostra equazione sarà
- A(x) = B(x).
Il che significa risolvere il sistema:
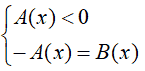
Quindi, la soluzione della nostra equazione è data dall'unione delle soluzioni dei due sistemi, ovvero:
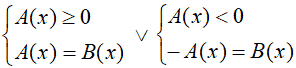
Esempio:
|1 - 2x| = 5x - 7.
Le soluzioni dell'equazione sono date dall'unione dei due sistemi:
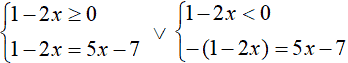
Iniziamo a risolvere il primo sistema:
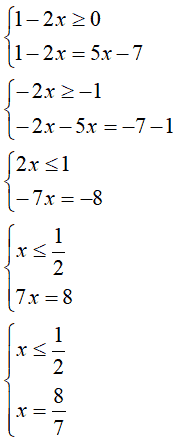
La soluzione trovata
x = 8/7
non è accettabile perché non è inferiore, o uguale, ad 1/2. Quindi il sistema non ammette soluzioni: potremmo dire anche che la soluzione del sistema è l'INSIEME VUOTO che indichiamo così
S = Ø.
Passiamo al secondo sistema:
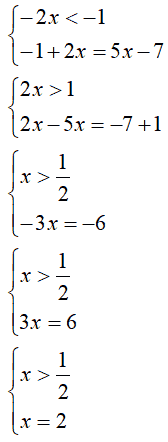
La soluzione trovata
x = 2
è accettabile perché è maggiore di 1/2.
Quindi la soluzione dell'equazione è
x = 2.
Così come abbiamo detto anche nelle precedenti lezioni, questo metodo di risoluzione si applica anche a tutte quelle equazioni che si presentano in una forma diversa rispetto a quella vista in precedenza, ma ad essa riconducibile.
Esempio:
|2 - x| + x2 = 4.
Basta portare x2 a secondo membro, ricordandoci di cambiare di segno, e avremo ricondotto la nostra equazione alla forma vista in precedenza:
|2 - x| = 4 - x2.
Ora risolviamo come di consueto:
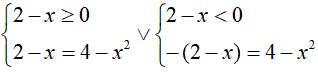
Iniziamo con il primo sistema:
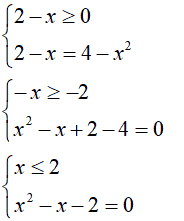
Risolviamo la seconda equazione del sistema:
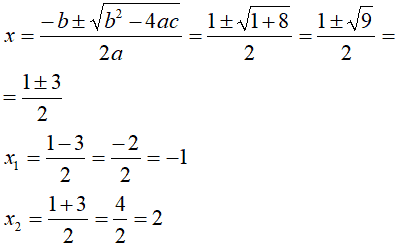
Entrambi i risultati ottenuti, - 1 e 2, sono risultati del sistema, in quanto rispondono alla condizione posta dalla disequazione presente nel sistema: infatti, uno è minore di due e l'altro è uguale a due.
Passiamo al secondo sistema:
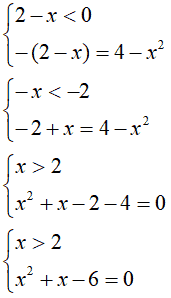
Risolviamo la seconda equazione del sistema:
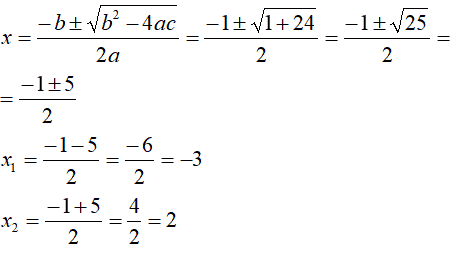
Nessuno dei due risultati ottenuti, - 3 e 2, è accettabile come soluzione del sistema, perché nessuno dei due risponde alla condizione posta dalla disequazione presente nel sistema, ovvero che la x sia maggiore di 2. Quindi la soluzione di questo sistema è l'insieme vuoto:
S = Ø.
Le soluzioni dell'equazione di partenza sono quindi:
x = -1 ˅ x = 2 .






