EQUAZIONI FRATTE CON VALORE ASSOLUTO
- Nozione di valore assoluto
- Equazioni con valore assoluto
- Equazioni frazionarie numeriche
- Equazioni con valore assoluto e lo zero
- Equazioni con valore assoluto ed una costante
- Equazioni con valore assoluto e incognita anche fuori dal modulo
- Equazioni con due moduli
- Equazioni con due moduli
- Equazioni con tre o più moduli
- Equazioni con un valore assoluto dentro l'altro
- Risoluzione di equazioni con valore assoluto
E se l'equazione con valore assoluto è anche fratta, come si risolve?
Innanzitutto ricordiamo che un'EQUAZIONE è FRATTA quando l'incognita è a denominatore.
Non ci sono regole particolari per la risoluzione delle equazioni fratte con valore assoluto. Quello che occorre fare è tenere conto delle regole:
- per la risoluzione delle equazioni fratte;
- per la risoluzione delle equazioni con valore assoluto che abbiamo appreso nelle lezioni precedenti.
Facciamo un esempio:
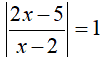
L'equazione che dobbiamo risolvere è del tipo
|A(x)| = k
con
k > 0
infatti
k = 1.
Noi sappiamo che, risolvere questo tipo di equazioni significa risolvere
A(x) = k ˅ A(x) = - k.
Nel nostro caso
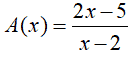
Quindi A(x) è una frazione e, affinché una frazione abbia significato, è necessario che il DENOMINATORE sia DIVERSO DA ZERO, in altre parole è necessario che
x - 2 ≠ 0
cioè
x ≠ 2.
Posta questa condizione andiamo a risolvere
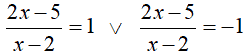
Iniziamo dalla prima equazione:
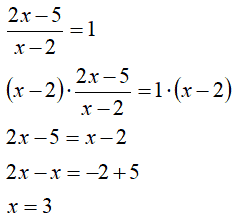
Questa prima soluzione è accettabile dato che è diversa da 2.
Passiamo alla seconda equazione:
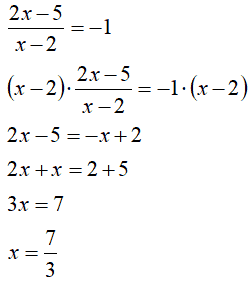
Anche questa seconda soluzione è accettabile dato che è diversa da 2.
Quindi le soluzioni della nostra equazione fratta con valore assoluto è:
x = 3 ˅ x = 7/3.
Facciamo un altro esempio:
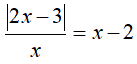
Trasformiamo la nostra equazione moltiplicando primo e secondo membro per x: per fare questo, però, dobbiamo porre la condizione che
x ≠ 0.
Posta la nostra condizione procediamo:
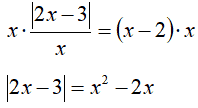
La nostra equazione è del tipo
| A(x)| = B(x).
Sappiamo che un'equazione di questo tipo si risolve ponendo
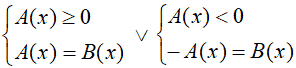
Quindi, noi dovremo risolvere
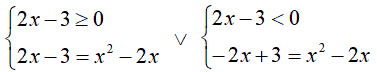
Partiamo con il primo sistema.
Iniziamo con la disequazione:
2x - 3 ≥ 0
2x ≥ 3
x ≥ 3/2.
Passiamo all'equazione:
2x - 3 = x2 - 2x
- x2 + 2x + 2x - 3 = 0
- x2 + 4x - 3 = 0
x2 - 4x + 3 = 0

Passiamo al secondo sistema.
Iniziamo con la disequazione:
2x - 3 < 0
2x < 3
x < 2/3.
Passiamo all'equazione:
- 2x + 3 = x2 - 2x
- x2 - 2x + 2x + 3 = 0
- x2 + 3 = 0
x2 - 3 = 0
x2 = 3

La soluzione della nostra equazione di partenza, quindi, è