EQUAZIONI CON VALORE ASSOLUTO ED UNA COSTANTE
- Nozione di valore assoluto
- Equazioni con valore assoluto
- Equazioni con valore assoluto e lo zero
- Equazioni con valore assoluto e incognita anche fuori dal modulo
- Equazioni con due moduli
- Equazioni con due moduli
- Equazioni con tre o più moduli
- Equazioni con un valore assoluto dentro l'altro
- Equazioni fratte con valore assoluto
- Risoluzione di equazioni con valore assoluto
Continuiamo l'esame dei vari tipi di EQUAZIONI CON VALORE ASSOLUTO e vediamo le equazioni nelle quali compaiono:
- in un membro il MODULO all'interno del quale è presente l'INCOGNITA;
- nell'altro membro una COSTANTE che chiameremo k.
La nostra equazione si presenterà nella forma:
|A(x)| = k.
A questo proposito è necessario distinguere due ipotesi:
- il caso in cui k è POSITIVO;
- il caso in cui k è NEGATIVO.
Non prendiamo in considerazione l'ipotesi in cui
k = 0
che abbiamo esaminato nella lezione precedente.
Partiamo dal primo caso, ovvero
k > 0.
Esempio:
|x| = 5
k = 5
quindi un valore positivo.
Ora chiediamoci: "Quand'è che il valore assoluto di x è uguale a 5?"
Questo avviene in due casi diversi:
- quando x è uguale a 5. Infatti il valore assoluto di 5 è 5;
- quando x è uguale a -5. Infatti il valore assoluto di -5 è sempre 5.
Quindi:
|x| = 5.
x = ± 5.
Quando abbiamo detto vale qualunque sia A(x).
Quindi, generalizzando, possiamo dire che, se ci troviamo di fronte ad un'equazione del tipo
|A(x)| = k.
con
k > 0
essa è verificata
- quando A(x) è uguale a k
- quando A(x) è uguale a -k.
In altre parole, la soluzione di
|A(x)| = k.
è data da
A(x) = k ˅ A(x) = - k
che si legge
A con x uguale k oppure a con x uguale meno k.
Esempio:
|4x + 2| = 10.
Nel nostro caso
k = 10
quindi un valore positivo.
Quindi, le soluzioni da noi cercate saranno:
4x + 2 = ±10.
Iniziamo col risolvere
4x + 2 = +10.
Avremo:
4x + 2 = +10
4x = +10 - 2
4x = 8
x = 8/4
x = 2.
Passiamo a risolvere
4x + 2 = -10.
Avremo:
4x + 2 = -10
4x = - 10 - 2
4x = - 12
x = -12/4
x = - 3.
Quindi, le nostre soluzioni sono:
x = - 3 ˅ x = 2.
Ora passiamo ad esaminare il caso in cui
k < 0.
Ricordiamo che, a primo membro abbiamo un MODULO, quindi sicuramente un valore positivo. Di conseguenza, qualunque valore assume la x, non si avrà mai che un valore positivo sia uguale ad uno negativo. Di conseguenza l'equazione è IMPOSSIBILE.
Quindi, ogni volta che
|A(x)| = k.
con
k < 0
l'equazione è impossibile. Quindi possiamo dire che
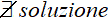
che si legge
non esiste soluzione
oppure
S = Ø
che si legge
la soluzione è l'insieme vuoto.
Esempio:
|x - 3| = -2.
Nel nostro caso
k = -2
quindi un valore negativo, di conseguenza l'equazione è impossibile.
L'equazione da risolvere potrebbe anche non essere scritta nella forma che abbiamo visto sopra, ma essere ad essa riconducibile.
Esempio:
|2x| - 4 = 0.
Portiamo -4 a secondo membro e cambiamo di segno:
|2x| = 4.
Abbiamo ricondotto l'equazione alla forma precedente e possiamo andare a risolverla.
Poiché
k = 4
quindi un valore positivo, le soluzioni saranno:
2x = ±4.
Partiamo col risolvere
2x = 4
x = 4/2
x = 2.
Passiamo a risolvere la seconda:
2x = - 4
x = - 4/2
x = -2.
Quindi, le nostre soluzioni sono:
x = - 2 ˅ x = 2.






