EQUAZIONI CON DUE MODULI
- Nozione di valore assoluto
- Equazioni con valore assoluto
- Equazioni con valore assoluto e lo zero
- Equazioni con valore assoluto ed una costante
- Equazioni con valore assoluto e incognita anche fuori dal modulo
- Equazioni con due moduli
- Equazioni con tre o più moduli
- Equazioni con un valore assoluto dentro l'altro
- Equazioni fratte con valore assoluto
- Risoluzione di equazioni con valore assoluto
Nella lezione precedente abbiamo visto come si risolvono EQUAZIONI nelle quali sono presenti DUE MODULI e soltanto quelli. In altre parole equazioni del tipo:
|A(x)| = |B(x)|.
E se, invece, l'equazione si dovesse presentare nella forma:
|A(x)| + |B(x)| = k
oppure
|A(x)| + |B(x)| = C(x)
come facciamo per risolverla?
Vediamolo alcuni esempi concreti attraverso i quali spiegheremo come si procede.
1° caso. Equazione del tipo:
|A(x)| + |B(x)| = k.
Esempio:
|x| + |x-3| = 5.
La prima cosa che dobbiamo fare è STUDIARE IL SEGNO delle ESPRESSIONI poste dentro ogni MODULO.
In altre parole andare a cercare:
- quando x è positivo, negativo o nullo;
- quando x- 3 è positivo, negativo o nullo.
Quindi:
x ≥ 0
e
x - 3 ≥ 0 da cui otteniamo x ≥ 3.
La seconda cosa da fare è RIPORTARE i RISULTATI ottenuti su un GRAFICO in modo da avere una chiara visione di insieme della situazione. Nel grafico indicheremo:
- con una linea continua i valori delle x che rendono positiva l'espressione;
- con una linea discontinua i valori delle x che rendono negativa l'espressione;
- con un pallino vuoto, i valori della x che annullano l'espressione.

Ora andiamo a SCRIVERE I SISTEMI che ci permetteranno di risolvere l'equazione.
Osserviamo che possiamo dividere il grafico in tre parti:

- quando x è minore di zero, entrambe le espressioni presenti nei moduli sono negative;
- quando la x è compresa tra zero e 3, l'espressione x- 3 è negativa, mentre l'espressione x è positiva;
- quando la x è maggiore di 3 entrambe le espressioni sono positive.
Questo equivale a risolvere tre sistemi:
- quando x è minore di zero, entrambe
le espressioni presenti nei moduli sono negative. Quindi si tratta di
risolvere il seguente sistema:
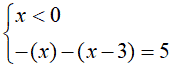
- quando la x
è compresa tra zero e 3,
l'espressione x- 3 è
negativa, mentre l'espressione
x è positiva. Quindi il sistema
da risolvere sarà:
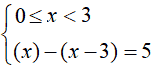
- quando la x è
maggiore di 3 entrambe
le espressioni sono positive. Il sistema da risolvere sarà:
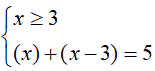
In altre parole, i tre sistemi sono costruiti ponendo:
- una disequazione che rappresenta la condizione;
- una equazione che dipende dal segno.
I risultati dell'equazione sono accettabili se viene rispettata la condizione posta dalla disequazione.
Una parola in più va spesa per gli estremi degli intervalli (nel nostro caso lo 0 e il 3). Essi possono essere inclusi, indifferentemente, in un intervallo o in quello successivo: bisogna, però, fare attenzione a non includerli in entrambi.
La soluzione della nostra equazione è data dall'unione dei tre risultati ottenuti.
Procediamo:
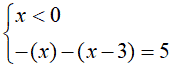
-(x) - (x-3) = 5
- x - x + 3 = 5
-2x = 5 - 3
-2x = 2
x = -2/2
x = -1.
La soluzione è accettabile poiché è minore di zero.
Passiamo al secondo sistema:
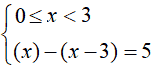
x - x + 3 = 5
x - x = 5 - 3
0 = 2.
Chiaramente la nostra equazione non è mai vera e il sistema non ammette soluzioni. Quindi
S = Ø.
Concludiamo con il terzo sistema:
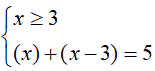
x + x - 3 = 5
2x = 5 + 3
2x = 8
x = 8/2
x = 4.
La soluzione è accettabile poiché è maggiore di 3.
Quindi, le soluzioni dell'equazione di partenza sono:
x = -1 ˅ x = 4.
2° caso. Equazione del tipo:
|A(x)| + |B(x)| = C(x).
Esempio:
|2x| - |3x + 1| = x.
Iniziamo a STUDIARE IL SEGNO delle ESPRESSIONI poste dentro ogni MODULO.
Quindi:
2x ≥ 0 da cui otteniamo x ≥ 0
3x + 1 ≥ 0 da cui otteniamo 3x ≥ -1 ovvero x ≥ -1/3.
Ora passiamo a RIPORTARE i RISULTATI ottenuti sul GRAFICO:
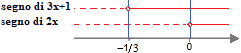
Quindi andiamo a SCRIVERE I SISTEMI che ci permetteranno di risolvere l'equazione:
- quando x
è minore di -1/3, entrambe le espressioni presenti nei moduli sono negative.
Quindi dobbiamo risolvere il sistema
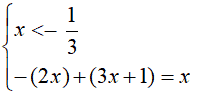
-2x + 3x + 1 = x
-2x + 3x - x = -1
-3x + 3x = -1
0 = -1.
L'equazione non è mai verificata. Quindi
S = Ø
- quando la x
è compresa tra -1/6 e 0 ,
l'espressione 3x
+ 1 è positiva, mentre l'espressione 2x
è negativa. Quindi dobbiamo risolvere il sistema
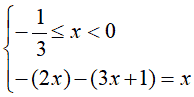
-2x - 3x - 1 = x
-2x - 3x - x = + 1
-6x = + 1
x = - 1/6.
La soluzione è accettabile perché è compresa nell'intervallo definito dalla disequazione presente nel sistema;
- quando la x
è maggiore di 0
entrambe le espressioni sono positive. Quindi dobbiamo risolvere il
sistema
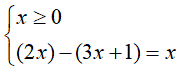
2x - 3x - 1 = x2x - 3x - x = 1
-2x = 1
x = -1/2.
La soluzione non è accettabile poiché non è maggiore o uguale a zero. Quindi
S = Ø.
La soluzione della nostra equazione di partenza quindi è
x = - 1/6.
Vediamo ancora un esempio riconducibile a questo secondo caso.
Esempio:
|x - 1|+ |x + 4| = 8 + x.
Partiamo con lo STUDIARE IL SEGNO delle ESPRESSIONI poste dentro ogni MODULO.
Quindi:
x - 1 ≥ 0 da cui otteniamo x ≥ 1
x + 4 ≥ 0 da cui otteniamo x ≥ - 4.
Ora passiamo a RIPORTARE i RISULTATI ottenuti sul GRAFICO:
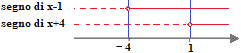
Ora andiamo a SCRIVERE I SISTEMI che ci permetteranno di risolvere l'equazione:
- quando x
è minore di - 4 , entrambe le
espressioni presenti nei
moduli sono negative. Quindi dobbiamo risolvere il sistema
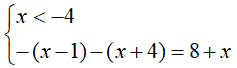
-x +1 - x - 4 = 8 + x
- x - x - x = 8 - 1 + 4
-3x = 11
x = -11/3.
La soluzione trovata non soddisfa la condizione che la x sia minore di -4. Quindi
S = Ø
- quando la x
è compresa tra -4 e
1,
l'espressione x - 1 è
positiva, mentre l'espressione
x + 4 è negativa. Quindi
dobbiamo risolvere il sistema
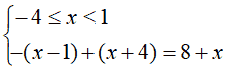
- x + 1 + x + 4 = 8 + x
- x + x - x = 8 - 1 - 4
- x = 3
x = -3.
La soluzione è accettabile perché è compresa tra - 4 e 1;
- quando la x
è maggiore di 1
entrambe le espressioni sono positive. Quindi dobbiamo risolvere il
sistema
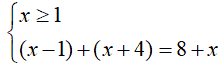
x - 1 + x + 4 = 8 + x
x + x - x = 8 - 4 + 1
x =5.
La soluzione è accettabile poiché 5 è maggiore di 1.
L'equazione di partenza ha, quindi, le seguenti soluzioni
x = -3 ˅ x = 5.
Il modo di procedere visto in questa lezione si applica anche nel caso in cui nell'equazione compaiono più di due moduli contenenti l'incognita. Nella prossima lezione vedremo un esempio riferito proprio a questo caso.






